Half Life

Pronunciation: /hæf laɪf/ Explain

The half life of a substance is the time it takes for 1/2 of the substance to decay, metabolize, or be used up. For example, if 1/2 of a drug is metabolized in 3 hours, after 6 hours 1/4 of the drug is left and 3/4 of the drug has been used:

After 9 hours, 1/8 of the drug is left: The half life formula is an exponential function: where D is the remaining substance after time t, D₀ is the initial amount of the substance, h is the half life of the substance, and t is the elapsed time.

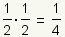
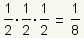
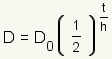
Graph of Half Life Function

Click on the blue points on the sliders and drag them to change the figure. What changes when D_0 changes? What changes when h changes?

Manipulative 1 - Half Life Created with GeoGebra.

Example

The half life of a radioactive substance is 3 hours. The initial amount is 3 grams. How long before only 0.6 grams is left?

Step	Equation	Description
1		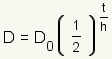Start with the half-life formula.
2		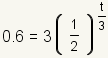Fill the values into the formula. The initial amount D0 = 3. The half-life h = 3. The amount left after t hours is D = 0.6. Solve for t.
3		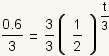Use the multiplication property of equality to multiply both sides of the equation by 1/3.
4		Use the logarithm to convert the equation from exponential form to logarithmic form. The definition of a logarithm is logab = c if and only if ac = b. In this case a = 1/2, b = 0.2 and c = t/3.
5		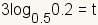Use the multiplication property of equality to multiply both sides of the equation by 3.
6		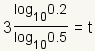Use the change of base formula to convert the logarithm to base 10. The change of base formula is 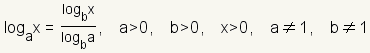. In this case, a = 1/2, x = 0.2 and b = 10.
7		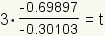Substitute the values of the logarithms into the equation. log100.2 ≈ -0.69897. log100.5 ≈ -0.30103.
8	t ≈ 6.9658	Calculate the approximate value of t. After about 7 hours there will only be 0.6 grams left.
Table 2: Half life example.

References

1. McAdams, David E.. All Math Words Dictionary, half-life. 2nd Classroom edition 20150108-4799968. pg 89. Life is a Story Problem LLC. January 8, 2015. Buy the book

Cite this article as:

McAdams, David E. Half Life. 4/22/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. http://www.allmathwords.org/en/h/halflife.html.

Image Credits

• All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.

Revision History

4/22/2019: Update equations and expressions to new format. (McAdams, David E.)
3/16/2019: Minor wording change. (McAdams, David E.)
12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
7/16/2018: Removed broken links, updated license, implemented new markup, implemented new Geogebra protocol. (McAdams, David E.)
10/25/2010: Expanded example and added description to example. (McAdams, David E.)
2/8/2010: Added "References". (McAdams, David E.)
11/26/2008: Change equations to images. Added graph (McAdams, David E.)
8/7/2008: Change equations to Hot_Eqn. (McAdams, David E.)
7/12/2007: Initial version. (McAdams, David E.)