Interest

Pronunciation: /ˈɪn.trɪst/ Explain

Interest is an amount paid based on the principal of a loan for the use of the money. When one borrows money, one is expected to pay it back to the lender, adding on interest.

The amount of money borrowed is called principal. If one borrows $100, the principal is $100.

The interest rate is the portion of the principle that is added as interest. For example, if the interest rate is 10% and the loan amount is £140, the interest amount is £14 (£140·0.10 = £14). Interest rates are typically given as an nominal interest rate per year.

If the interest is compounded more than once a year, the actual interest rate is more than the nominal interest rate. This rate is called the annual interest rate. To convert a nominal interest rate to an annual interest rate, use the formula 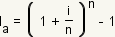where i_a is the annualized interest rate, i is the nominal interest rate, and n is the number of times per year the interest is compounded. 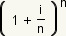The part of the equation is called the accumulation factor. The accumulation factor is a measure of how fast the principle grows. The greater the accumulation factor, the faster the principle grows.

The interest on first mortgages on homes usually runs from about 5% to 18%. Interest on credit cards can run from 10% to 36%. Interest on payday loans and title loans often runs as high as 1500%.

Variables

The variables that are used for calculation of interest in this article are:

Variable	Description
I	Interest
r	Rate of interest
P0	Initial principal
t	Number of periods elapsed (time)
Table 1: Descriptions of variables

Simple Interest

In simple interest, the interest is not added into the principal each period, but tracked separately. The formula for simple interest for a single period is I = P₀·r. The formula for simple interest for multiple periods is I = (P₀·r)·t. Typically, interest is rounded to the nearest two decimal digits.

Example 1: What is the interest on a loan of £120 at a rate of 7%?
I = P₀·r, P₀ = £120, r = 7%
I = £120·0.07 (7% = 0.07. See Percent.)
I = £8.40

Example 2: What is the interest on $1,423.67 at a rate of 8.7%?
I = P₀·r, P₀ = $1,423.67, r = 8.7%
I = $1,423.67·.087 = $123.85929
I = 123.86 (Round to two decimal places.)

Compound Interest

Compound interest is interest calculated using both principal and accrued interest. Table 1 show the compounding of interest on $100 at 1% per month.

Month	Starting Principal	Interest	Ending Principal
1	100.00	1.00	101.00
2	101.00	1.01	102.01
3	102.01	1.02	103.03
4	103.03	1.03	104.06
5	104.06	1.04	105.10
6	105.10	1.05	106.15
7	106.15	1.06	107.21
8	107.21	1.07	108.28
9	108.28	1.08	109.36
10	109.36	1.09	110.45
11	110.45	1.10	111.55
12	111.55	1.12	112.67
Table 2 - Compound interest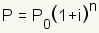

The simplest equation for compound interest is where P₀ is the initial principal, i is the interest rate per period, and n is the number of periods. Plugging the example from table 1 into the equation gives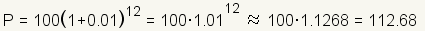

Note that the result from using the table 1 is 112.67 and the result from using the formula is 112.68. The equation is more accurate than the table.

Another equation used with compound interest is . This equation is used if the interest is given as an annual interest, but compounds monthly. Most home mortgages in the United States use this interest formula.

In order to make interest rates comparable, interest rates can be annualized. The formula for annualizing interest rates is , where i_a is the annualized interest rate, i is the interest rate and n is the number of times per year interest is compounded.

Graphs of Compound Interest

Click on the blue points on the sliders to change the figure. Manipulative 1 - Compound Interest Created with GeoGebra.

Click on the blue point on the slider in manipulative 1 to change the interest rate. Discovery Move the blue point on the slider until the value at year 10 is $2. Since $2 is twice $1, the starting value, the money has doubled in 10 years. At what interest rate does the money double in 10 years? At what interest rate does the money triple in 10 years? At what interest rate does the money quadruple in 10 years? At what interest rate does the money increase 5 times in 10 years? At what interest rate does the money increase 6 times in 10 years?

Continuous Compounding

Click on the blue point in the slider and drag it to change the figure. Manipulative 2 - Continuous Compounding Created with GeoGebra.

Continuous compounding assumes interest is compounded continuously. This can be calculated using the equation . In this equation A represents the accumulated principal and interest, P represents the initial principal, e is Euler's number, i represents the interest rate, and t represents the time in years. The graph in manipulative 2 shows continuous compounding. Click on the slider labeled i and drag it to change the interest rate.

References

1. McAdams, David E.. All Math Words Dictionary, interest. 2nd Classroom edition 20150108-4799968. pg 100. Life is a Story Problem LLC. January 8, 2015. Buy the book

Cite this article as:

McAdams, David E. Interest. 3/22/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. http://www.allmathwords.org/en/i/interest.html.

Image Credits

• All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.

Revision History

3/22/2019: Corrected wording. (McAdams, David E.)
12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
8/6/2018: Removed broken links, updated license, implemented new markup, implemented new Geogebra protocol. (McAdams, David E.)
6/13/2010: Added accumulation factor. (McAdams, David E.)
5/21/2010: Rewrote first few paragraphs for clarification. (McAdams, David E.)
2/18/2010: Rewrote article and included article 'Compound Interest'. (McAdams, David E.)
11/29/2008: Initial version. (McAdams, David E.)