Kite
Pronunciation: /kaɪt/ Explain
|
A kite is a quadrilateral with two sets of adjacent, congruent sides. Properties of a Kite
|
Construction of the Incircle of a Kite
| Step | Diagram | Description |
|---|---|---|
| 1 | 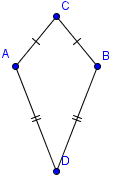 | Start with a convex kite. |
| 2 | 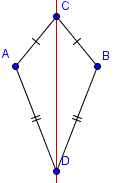 | Construct the angular bisector of one of the angles connecting congruent sides. |
| 3 | 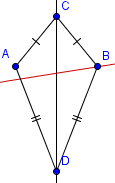 | Construct the angular bisector of one of the angles connecting non-congruent sides. |
| 4 | 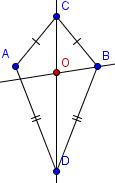 | Label the intersection of bisectors from steps 2 and 3 as O. |
| 5 | 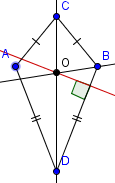 | Construct a line through O perpendicular to one of the sides. |
| 6 | 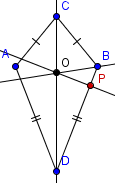 | Label the intersection of the line constructed in step 5 with the side to which it is perpendicular as P. |
| 7 | 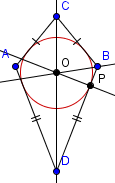 | Construct a circle with center O and radius OP. |
| Table 1 | ||
Geometric Figure Made with Kites
| Image | Description |
|---|---|

| This tessellation using kites is called a deltoidal trihexagonal tiling. To construct this tessellation, divide each hexagon into six kites by drawing a segment from the midpoint of each side to the center. Then tesselate the divided hexagon so that three hexagons share each vertex. |
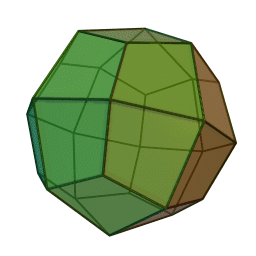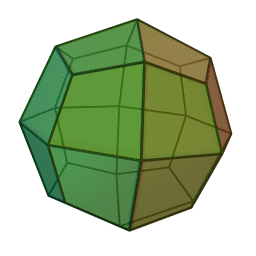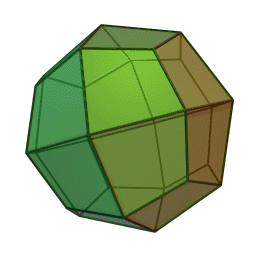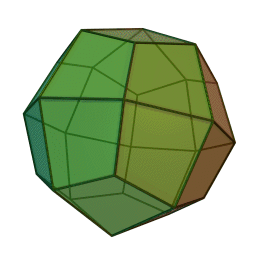
| A deltoidal icositetrahedron is a polyhedron whose faces are kites. Click to print a net of a deltoidal icositetrahedron to cut out and paste together. |
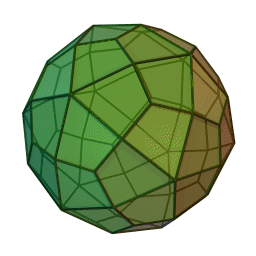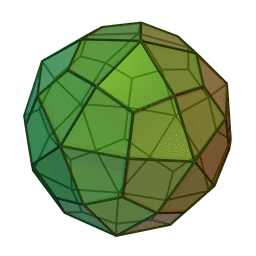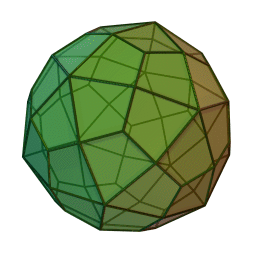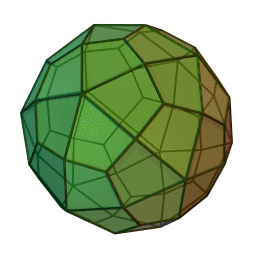
| A deltoidal hexecontrahedron is a polyhedron whose faces are kites. |
References
- McAdams, David E.. All Math Words Dictionary, kite. 2nd Classroom edition 20150108-4799968. pg 105. Life is a Story Problem LLC. January 8, 2015. Buy the book
More Information
- McAdams, David E.. Kite. lifeisastoryproblem.com. Life is a Story Problem LLC. 8/7/2018. http://www.lifeisastoryproblem.com/explore/kite.html.
Cite this article as:
McAdams, David E. Kite. 12/21/2018. All Math Words Encyclopedia. Life is a Story Problem LLC. http://www.allmathwords.org/en/k/kite.html.Image Credits
- All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
- Deltoidal Hexecontrahedron: Maxim Razin, https://commons.wikimedia.org. This file is licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license. https://commons.wikimedia.org/wiki/File:Deltoidalhexecontahedron.jpg.
- Deltoidal Icositetrahedron: Cyp, https://commons.wikimedia.org. This file is licensed under the Creative Commons Attribution-Share Alike 3.0 Unported license. https://commons.wikimedia.org/wiki/File:Deltoidalicositetrahedron.gif.
- Deltoidal Trihexagon Tiling: R. A. Nonenmacher, https://commons.wikimedia.org. Image licensed under GNU Free Documentation License. https://commons.wikimedia.org/wiki/File:Tiling_Dual_Semiregular_V3-4-6-4_Deltoidal_Trihexagonal.svg.
Revision History
12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)8/29/2018: Corrected spelling. (McAdams, David E.)
8/7/2018: Removed broken links, updated license, implemented new markup, implemented new Geogebra protocol. (McAdams, David E.)
3/4/2010: Added "References", Geometric figure made from kites. (McAdams, David E.)
12/13/2008: Added vocabulary links, properties of a kite, and construction of the incircle of a kite. (McAdams, David E.)
9/16/2008: Initial version. (McAdams, David E.)
- Navigation
- Home
- Contents
-
# A B C D E F G H I J K L M N O P Q R S T U V W X Y Z - Teacher Aids
- Classroom Demos
- How To
- LIASP
- LIASP Home
- Conditions of Use
- Privacy Policy
- Donate to LIASP
- Help build this site
- About LIASP
- Contact LIASP
All Math Words Encyclopedia is a service of
Life is a Story Problem LLC.
Copyright © 2018 Life is a Story Problem LLC. All rights reserved.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License
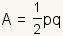 where p is the length of one diagonal and q is the
length of the other diagonal. See manipulative 1.
where p is the length of one diagonal and q is the
length of the other diagonal. See manipulative 1.