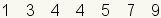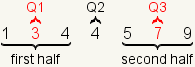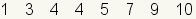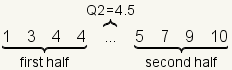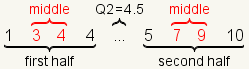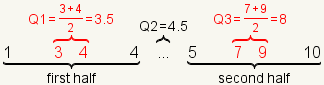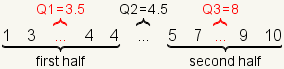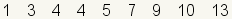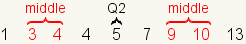Quartile

Pronunciation: /ˈkwɔr.taɪl/ Explain

Data set { 1, 3, 4, 4, 5, 7, 9 } where 3 is the first quartile, the second 4 is the second quartile or median, and 7 is the third quartile.
Figure 1: Quartiles

Data set { 1, 3, 4, 4, 5, 7, 9, 10, 10 } where the first quartile is (3+4)/2=3.5, the second quartile or median is the 5, and the third quartile is (9+10)/2=9.5.
Figure 2: Quartiles

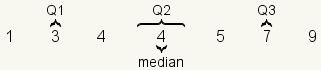
A quartile is one of three values that divides a dataset into four groups. Each group has the same number of elements. The first quartile, also called Q1, is a number between the lowest fourth of the dataset and the 2nd fourth. The second quartile, also called Q2, is a number between the 2nd fourth of the dataset and the 3rd fourth. The second quartile (Q2) is the same as the median of the dataset. The third quartile, also called Q3, is a number between the 3rd fourth and the 4th fourth.

Quartiles and Percentiles

QuartilePercentile
Q125th
Q2 or median50th
Q375th
Table 1: Quartile and percentile.

The first quartile, Q1, is the same as the 25th percentile. The second quartile, Q2, is the same as the 50th percentile. The third quartile, Q3 is the same as the 75th percentile.

Calculating Quartiles

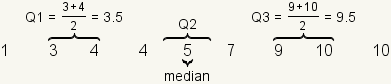
To find the quartiles of a dataset, first find the median of the dataset. If the dataset has an odd number of elements, use the middle number. If the dataset has an even number of elements, use the arithmetic mean of the two middle numbers. This splits the dataset into two equal parts. Neither part contains the median. The median is the same as Q2.

Then take each half of the dataset and find the median of that half. The median of the first half of the dataset is Q1. The median of the second half of the dataset is Q3.

Examples

StepFigureDescription
1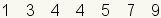1 3 4 4 5 7 9This is the dataset to divide into quartiles.
21 3 4 4 5 7 9 with the second 4 identified as the middle.Since the dataset has an odd number of elements, pick the middle element for the median (Q2).
31 3 4 4 5 7 9 with 1 3 4 identified as the first half, 4 identified as Q2, and 5 7 9 identified as the second half.The middle number divides the dataset into two halves. Since the middle number is the median, it is not included in either half.
4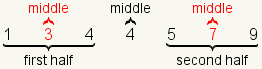1 3 4 4 5 7 9 with 1 3 4 identified as the first half and 3 is identified as the middle of the first half, 4 identified as Q2, 5 7 9 identified as the second half with 7 identified as the middle of the second half.Since each half contains an odd number of elements, pick the middle number in each half.
5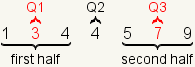1 3 4 4 5 7 9 with 3 identified as Q1, the second 4 identified as Q2, and 7 identified as Q3.The middle of the first half and second half are Q1 and Q3 respectively.
Table 2: Example 1

StepFigureDescription
1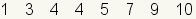1 3 4 4 5 7 9 10This is the dataset to divide into quartiles.
21 3 4 4 5 7 9 10 with the second 4 and 5 identified as the middle.Since the dataset has an even number of elements, pick the middle two elements to calculate the median (Q2).
3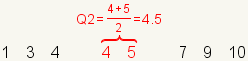1 3 4 4 5 7 9 10 with the second 4 and 5 identified as the middle. Q2 is calculated as (4+5)/2=4.5.The median (Q2) is the arithmetic mean of the middle two numbers.
4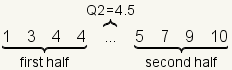1 3 4 4 5 7 9 10 with 1 3 4 4 identified as the first half, 4.5 identified as Q2, and 5 7 9 10 identified as the second half.The middle number divides the dataset into two halves. The two numbers used to calculate the median are included in the halves.
5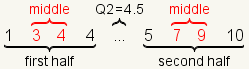1 3 4 4 5 7 9 10 with 1 3 4 4 identified as the first half and 3 4 is identified as the middle of the first half, 4.5 identified as Q2, 5 7 9 10 identified as the second half with (7+9)/2=8 identified as Q3.Since each half contains an even number of elements, pick the middle two numbers in each half.
6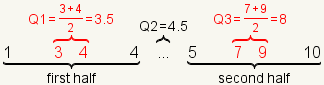1 3 4 4 5 7 9 10 with 1 3 4 4 identified as the first half and (3+4)/2=3.5 is identified as Q1, 4.5 identified as Q2, 5 7 9 10 identified as the second half with 8 identified as Q3.Calculate Q1 as the arithmetic mean of the middle two numbers of the first half. Calculate Q3 as the arithmetic mean of the middle two numbers of the second half.
7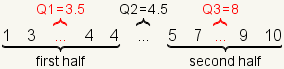1 3 4 4 5 7 9 10 with 1 3 4 4 identified as the first half and (3+4)/2=3.5 is identified as Q1, 4.5 identified as Q2, 5 7 9 10 identified as the second half with 8 identified as Q3.For this dataset Q1=3.5, Q2=4.5, and Q3=8.
Table 3: Example 2

StepFigureDescription
1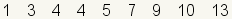1 3 4 4 5 7 9 10 13This is the dataset to divide into quartiles.
21 3 4 4 5 7 9 10 13 with 5 identified as the middle.Since the dataset has an odd number of elements, pick the middle element as the median.
31 3 4 4 5 7 9 10 with 5 identified as the Q2.Q2 is the same as the median.
4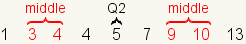1 3 4 4 5 7 9 10 with 1 3 4 4 identified as the first half, 3 4 identified as the middle of the first half, 5 identified as Q2, and 7 9 10 13 identified as the second half, and 9 10 identified as the middle of the second half.Q2 divides the dataset into two halves. Since the halves have an even number of elements each, pick the middle two numbers of the halves.
51 3 4 4 5 7 9 10 with 1 3 identified as the first quarter, 3.5 identified as Q1, 4 4 identified as the second quarter, 4.5 identified as Q2, 5 7 identified as the third quarter, 9.5 identified as Q3, and 9 10 identified as the third quarter.Calculate Q1 and Q3 as the arithmetic mean of the middle two numbers.
Table 4: Example 3

References

  1. McAdams, David E.. All Math Words Dictionary, quartile. 2nd Classroom edition 20150108-4799968. pg 148. Life is a Story Problem LLC. January 8, 2015. Buy the book

Cite this article as:

 McAdams, David E. Quartile. 12/21/2018. All Math Words Encyclopedia. Life is a Story Problem LLC. http://www.allmathwords.org/en/q/quartile.html.

Image Credits

Revision History

12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
12/3/2018: Removed broken links, updated license, implemented new markup. (McAdams, David E.)
1/12/2009: Initial version. (McAdams, David E.)

All Math Words Encyclopedia is a service of Life is a Story Problem LLC.
Copyright © 2018 Life is a Story Problem LLC. All rights reserved.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License