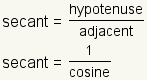Secant (Trigonometry)

Pronunciation: /ˈsi.kænt/ Explain

Click on the blue points and drag them to change the figure Manipulative 1 - Secant Created with GeoGebra.

Secant is defined to be equal to the length of the hypotenuse divided by the length of the side adjacent to the angle. This is also equal to the multiplicative inverse of the cosine function.

Figure 1: Secant equations.

References

1. McAdams, David E.. All Math Words Dictionary, secant. 2nd Classroom edition 20150108-4799968. pg 161. Life is a Story Problem LLC. January 8, 2015. Buy the book

More Information

• McAdams, David E.. Cosine. allmathwords.org. All Math Words Encyclopedia. Life is a Story Problem LLC. 3/12/2009. http://www.allmathwords.org/en/c/cosine.html.

Cite this article as:

McAdams, David E. Secant (Trigonometry). 12/21/2018. All Math Words Encyclopedia. Life is a Story Problem LLC. http://www.allmathwords.org/en/s/secant.html.

Image Credits

• All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.

Revision History

12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
12/6/2018: Removed broken links, updated license, implemented new markup, implemented new Geogebra app. (McAdams, David E.)
8/7/2018: Changed vocabulary links to WORDLINK format. (McAdams, David E.)
12/31/2008: Added equations. (McAdams, David E.)
11/1/2008: Changed manipulative to GeoGebra. (McAdams, David E.)
4/30/2008: Initial version. (McAdams, David E.)