Número binario: Un número expresado en un conjunto de cuenta de la base 2 que utiliza 1 y 0 como los únicos dígitos.

Número binario

Un número binario es un número expresado en un sistema de cuenta de la base 2. En un sistema de cuenta de la base 2, hay solamente 2 dígitos: 0 y 1.

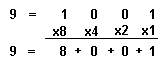9 = 1001 base 2, 9 = 1x8 + 0x4 + 0x2 + 1x1
Figura 1:910 = 10012

El cuadro 1 ilustra que 9 en devérticel (base 10) es igual a 1001 en el binario (base 2). En devérticel, los primeros cuatro valores de lugar a la izquierda del devérticel son:
1 = 100,
10 = 101,
100 = 102, y
1000 = 103.
En devérticel (base 10), cada valor de lugar es 10 veces el valor de lugar anterior.

En binario los primeros cuatro valores de lugares son:
1 = 20,
2 = 21,
4 = 22, y
8 = 23.
En binario (base 2) cada valor de lugar es 2 veces el valor de lugar anterior. Tan 10012 = 1·8 + 0·4 + 0·2 + 1·1 = 9.

Decir números en binario

Al leer números en binario, no utilice los términos “ciento� y “mil�. Estas palabras se definen solamente para la numeración devérticel. se dice 10012, “una oh oh una base dos�. Al hablar, la palabra “oh� es corta para cero.

Más información

  • McAdams, David E. Binario. AllMathWords.org. Life is a Story Problem.org. 2009-04-03. http://www.allmathwords.org/article.aspx?lang=es&id=Binary.
  • binario. buscon.rae.es. Real Academia Española. 2009-04-03. http://buscon.rae.es/draeI/SrvltConsulta?TIPO_BUS=3&LEMA=binario.

Citar este artículo como:
Número binario. 2009-04-03. Enciclopedia de Todas las Palabras de la Matemáticas. Life is a Story Problem.org. http://www.allmathwords.org/es/b/binarynumber.html.

Traducciones

créditos de imagen

  • Todas las imágenes y manipulatives están por David McAdams a menos que estén indicadas de otra manera. Todas las imágenes de David McAdams son & de los derechos reservados; © Life is a Story Problem.org y se puede reproducir para el uso educativo no comercial solamente.

La historia de revisión


2009-04-03: Traducido automáticamente por BabelFish. (babelfish.yahoo.com.)
2008-06-24: Esquema de color cambiado (McAdams, David.)
2008-04-18: Versión inicial (McAdams, David.)

Enciclopedia de Todas las Palabras de la Matemáticas es un servicio de Life is a Story Problem.org.
Los derechos reservados ©2005-2009 de Life is a Story Problem.org. Todos los derechos reservados.
Creative Commons License Este trabajo se autoriza debajo de una Creative Commons Attribution-Noncommercial-Share Alike 3.0 License