Enciclopedia de Todas las Palabras de la Matemáticas Home Page -

Circunferencia

Un circunferencia es todos los puntos en un plano que son una distancia dada del punto central. Al usar un compás para dibujar un circunferencia, es el punto del compás el centro del circunferencia, y la aguja marca todos los puntos que sean la misma distancia del centro.

Cuadro 1 - Usando un compás para dibujar un circunferencia.
Cortesía de imagen de GeoTeach.com.

Partes de un circunferencia

Chasque encendido los puntos azules en el manipulante 1 y arrástrelos para cambiar la figura.

Lo sentimos, pero la GeoGebra Applet no se pudo iniciar. Por favor, asegúrese de que Java 1.4.2 (o posterior) está instalado y activo en su navegador ( Haga clic aquí para instalar Java ahora )

El manipulante 1: Partes de un circunferencia. Creado con GeoGebra.

El centro circunferencia es el punto de el cual todos los puntos del circunferencia son equidistantes.
Un radio de un circunferencia es una recta segmento del centro del circunferencia a uno de los puntos en el circunferencia.
Un diámetro de un circunferencia es recta segmento a partir de un punto en el circunferencia al lado opuesto a través del centro del circunferencia. La longitud de un diámetro es dos veces la longitud de un radio (d = 2r).
La circunferencia de un circunferencia es el borde del circunferencia. La circunferencia puede también referir a la longitud del borde del circunferencia.
Un cuerda de un circunferencia es una recta segmento de cualquier punto en el circunferencia a cualquier otro punto en el circunferencia. Vea el cuerda.
Un arco es una porción de la circunferencia del circunferencia.

Cheque de comprensión

¿Es un diámetro también un cuerda? Intente mover las puntos finales del cuerda en el cuadro 2 envértice de las puntos finales del diámetro.
Sí.
Correcto. Puesto que un cuerda es una recta entre cualquier dos puntos en el circunferencia, y un diámetro es una recta entre un punto y un punto enfrente de ese punto, un diámetro es un caso especial de un cuerda.
No.
Incorrecto. Puesto que un cuerda es una recta entre cualquier dos puntos en el circunferencia, y un diámetro es una recta entre un punto y un punto enfrente de ese punto, un diámetro es un caso especial de un cuerda.
¿Cada circunferencia tiene exactamente un diámetro? Intente mover las puntos finales del diámetro en el cuadro 2.
Sí.
Incorrecto. Cada circunferencia tiene un número infinito de puntos en su circunferencia, él también tiene un número infinito de diámetros. Sin embargo, todos los diámetros de un circunferencia tienen la misma medida.
No.
Correcto. Cada circunferencia tiene un número infinito de puntos en su circunferencia, él también tiene un número infinito de diámetros. Sin embargo, todos los diámetros de un circunferencia tienen la misma medida.
¿Cuál es la relación entre la medida de un radio y la medida de un diámetro de un circunferencia?
La medida de un radio no tiene ninguna relación a la medida de un diámetro.
Incorrecto. Un radio va a medio camino a través de un circunferencia. Un diámetro va hasta el final a través de un circunferencia. La medida de un radio es tan el 1/2 la medida de un diámetro.
La medida de un radio es 1/4 de la medida de un diámetro.
Incorrecto. Un radio va a medio camino a través de un circunferencia. Un diámetro va hasta el final a través de un circunferencia. La medida de un radio es tan el 1/2 la medida de un diámetro.
La medida de un radio es el 1/2 la medida de un diámetro.
Correcto. Un radio va a medio camino a través de un circunferencia. Un diámetro va hasta el final a través de un circunferencia. La medida de un radio es tan el 1/2 la medida de un diámetro.
La medida de un radio es exactamente igual que la medida de un diámetro.
Incorrecto. Un radio va a medio camino a través de un circunferencia. Un diámetro va hasta el final a través de un circunferencia. La medida de un radio es tan el 1/2 la medida de un diámetro.

Fórmulas relacionadas con un circunferencia

Ecuaciones para un circunferencia
Definiciones de variables
Variable	Representa
r	radio
d	diámetro
c	circunferencia
a	área
h	x-coordine del centro de un circunferencia
k	y-coordine del centro de un circunferencia
Descripción	Ecuación
Diámetro de un circunferencia	d = 2r
Circunferencia de un circunferencia	c = 2πr
�?rea de un circunferencia	a = πr²
Ecuación para un circunferencia en coordenadas cartesianos	(x - h)² + (y - k)² = r²
Ecuación de un circunferencia con el centro en el origen en coordenadas polares	r = r₀

Lo sentimos, pero la GeoGebra Applet no se pudo iniciar. Por favor, asegúrese de que Java 1.4.2 (o posterior) está instalado y activo en su navegador ( Haga clic aquí para instalar Java ahora )

El manipulantes 2: Ecuación de un circunferencia. Creado con GeoGebra.

Chasque encendido los puntos en los resbaladores en el manipulantes 2 y arrástrelos para cambiar la figura.

Trazar un circunferencia

Para este uso de la demostración la ecuación siguiente para un circunferencia: (x + 1)² + (y - 2)² = (1.5)².

Trazar un circunferencia
Paso	Diagrama	Descripción
1		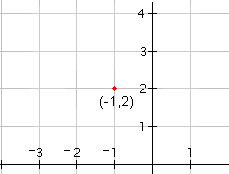Desde `x - h = x + 1`, `h = -1`. Desde `y - k = y - 2`, `k = 2.` El centro del circunferencia está tan en el punto `(- 1.2)`. Trace el punto `(-1.2)`.
2		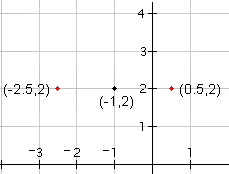Ahora dibuje los dos puntos que están en el circunferencia al derecho y a la izquierda del centro. Puesto que el radio es `1.5`, el punto izquierdo estará en `(-1 - 1.5, 2) = (-2.5, 2)` (x-coordine del centro del circunferencia menos el radio). El punto correcto estará en `(-1 + 1.5, 2) = (0.5, 2)` (y-coordine del centro del circunferencia más el radio).
3		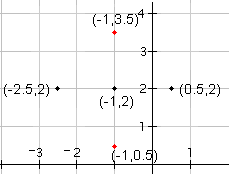Ahora dibuje los dos puntos que están en el circunferencia que está en la tapa y la parte inferior del centro. Puesto que el radio es `1.5`, el punto superior estará en `(-1, 2 + 1.5) = (-1, 3.5)` (y-coordine del centro del circunferencia más el radio). El punto inferior estará en `(-1, 2 - 1.5) = (-1.0.5)` (y-coordine del centro del circunferencia menos el radio).
4		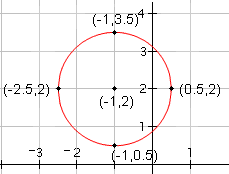Ahora dibuje un circunferencia a través de los cuatro puntos.

Más información

McAdams, David. Sección cónica. AllMathWords.org. Life is a Story Problem.org. 2009-04-03. http://www.allmathwords.org/article.aspx?lang=es&id=Conic%20Section.
McAdams, David. Centro de un circunferencia. AllMathWords.org. Life is a Story Problem.org. 2009-04-03. http://www.allmathwords.org/article.aspx?lang=es&id=Center%20of%20a%20Circle.
McAdams, David. Pi. AllMathWords.org. Life is a Story Problem.org. 2009-04-03. http://www.allmathwords.org/article.aspx?lang=es&id=Pi.

Citar este artículo como:

Circunferencia. 2009-04-03. Enciclopedia de Todas las Palabras de la Matemáticas. Life is a Story Problem.org. http://www.allmathwords.org/es/c/circle.html.

Traducciones

Click here to see this article in English.

créditos de imagen

Todas las imágenes y manipulatives están por David McAdams a menos que estén indicadas de otra manera. Todas las imágenes de David McAdams son & de los derechos reservados; © Life is a Story Problem.org y se puede reproducir para el uso educativo no comercial solamente.

La historia de revisión

2009-04-03: Traducido automáticamente por BabelFish. (babelfish.yahoo.com.)
2008-11-25: Acoplamiento agregado a chord.html en '' partes de un círculo '' (McAdams, David.)
2008-10-27: Manipulante cambiada bloc de bocetos de s del geómetra '' al geogebra. Fórmula corregida para el área de un círculo. Manipulante agregada para la ecuación de un círculo (McAdams, David.)
2008-04-28: Sección agregada en trazar un círculo. Sección cónica agregada a más Info (McAdams, David.)
2007-07-12: Versión inicial (McAdams, David.)

#	A	B	C	D
E	F	G	H	I
J	L	M	N	O
P	Q	R	S	T
U	V	X	Y

Enciclopedia de Todas las Palabras de la Matemáticas es un servicio de Life is a Story Problem.org.
Los derechos reservados ©2005-2009 de Life is a Story Problem.org. Todos los derechos reservados.
Este trabajo se autoriza debajo de una Creative Commons Attribution-Noncommercial-Share Alike 3.0 License