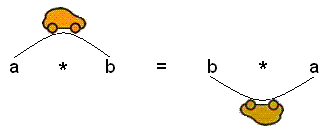Comutativo: Para un operador binario *, a * b = b * A.

Comutativo

Una operación binaria “*� es comutativa si a * b = b * a. En este ejemplo, “*� puede representar cualquier operación binaria.

Algunas operaciones binarias que son comutativas son:

  • Adición: a + b = b + a.
  • Multiplicación: a × b = b × a.

Algunas operaciones binarias que no son comutativas son:

  • Substracción: a - b ≠ b - a. Ejemplo: 3 - 2 ≠ 2 - 3: 1 ≠ -1.
  • Multiplicación de la matriz: A·B ≠ B·A.

historieta que demuestra la propiedad comutativa de la suma como “conmutación� a donde estaba b.
Cuadro 1 - Característica comutativa de un operador binario

Una forma para recordar “comutativo� es utilizar la palabra de raíz, “conmuta�. Conmute los medios de viajar a partir de un lugar a otro, tales como conmutación al trabajo. Tan en una operación binaria que sea comutativa, la variable “a� conmuta a donde estaba el “b�, y el “b variable� conmuta a donde estaba la “a�.

Más información

  • McAdams, David. Propiedad comutativa de la suma. AllMathWords.org. Life is a Story Problem.org. 2009-04-03. http://www.allmathwords.org/article.aspx?lang=es&id=Commutative%20Property%20of%20Addition.
  • McAdams, David. Propiedad comutativa de la multiplicación. AllMathWords.org. Life is a Story Problem.org. 2009-04-03. http://www.allmathwords.org/article.aspx?lang=es&id=Commutative%20Property%20of%20Multiplication.
  • McAdams, David. Binario. AllMathWords.org. Life is a Story Problem.org. 2009-04-03. http://www.allmathwords.org/article.aspx?lang=es&id=Binary.

Citar este artículo como:
Comutativo. 2009-04-03. Enciclopedia de Todas las Palabras de la Matemáticas. Life is a Story Problem.org. http://www.allmathwords.org/es/c/commutative.html.

Traducciones

créditos de imagen

  • Todas las imágenes y manipulatives están por David McAdams a menos que estén indicadas de otra manera. Todas las imágenes de David McAdams son & de los derechos reservados; © Life is a Story Problem.org y se puede reproducir para el uso educativo no comercial solamente.

La historia de revisión


2009-04-03: Traducido automáticamente por BabelFish. (babelfish.yahoo.com.)
2008-07-07: Ejemplo agregado (McAdams, David.)
2008-04-22: Versión inicial (McAdams, David.)

Enciclopedia de Todas las Palabras de la Matemáticas es un servicio de Life is a Story Problem.org.
Los derechos reservados ©2005-2009 de Life is a Story Problem.org. Todos los derechos reservados.
Creative Commons License Este trabajo se autoriza debajo de una Creative Commons Attribution-Noncommercial-Share Alike 3.0 License