Teorema de existencia

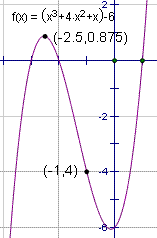
Un teorema de existencia es un teorema que prueba la existencia de una entidad o de entidades sin decir son cuántas entidades allí o cómo encontrarlas. En ejemplo de la existencia un teorema es ése para todos los polinomios, si un valor del polinomio es positivo para un valor de x, y la negativa para otro valor de x, después el valor del polinomio debe ser cero en alguna parte entre los dos valores del x.

En el cuadro 1, se trazan los puntos (-2.5, 0.875) y (-1, -4). Puesto que f(-2.5) es positiva, y f(-1) es negativa, entonces para un cierto valor de x, -2.5 < x < 0.875, f(x)=0. Note que este teorema no dice está para cuántos valores de x que f(x) es cero, ni de cómo encontrar el valor de f(x).