Función recíproca: Una relación que, para cada salida de la función, vuelve la entrada de la función.

Función recíproca

Una función recíproca es una relación que, dada la salida de la función, vuelve la entrada de la función. Mire las dos tablas abajo. La función representada como función 1 es lo recíproca de la función representada como función 2.

Función 1
f(x) = y
f(1.0) = 2.5
f(2.2) = 3.7
f(4.6) = 5.2
f(6.8) = 9.7
Función 2
f-1(y) = x
f-1(2.5) = 1.0
f-1(3.7) = 2.2
f-1(5.2) = 4.6
f-1(9.7) = 6.8

Indicado matemáticamente:

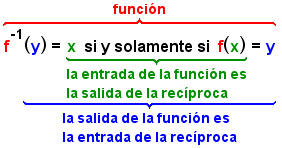f^ (- 1) (x) = y si y solamente si f (y)=x
Cuadro 1: Lo recíproca de una función.

Caja de chequeCheque de comprensión

Dado la función f y g, chasque “sí� la caja de cheque si son lo recíproca, o “no� la caja de cheque si no son.
f(12) = -1g(-1) = 12Sí No Correcto. Puesto que la entrada de cada función es la salida de la otra función, las funciones son la recíproca de uno a.Incorrecto. Puesto que la entrada de cada función es la salida de la otra función, las funciones son la recíproca de uno a.
f(1.5) = 2g(1.5) = 2Sí No Incorrecto. Puesto que la entrada f es 1.5 y la salida es 2, y la entrada de g es 1.5, estas dos funciones no son la recíproca de uno a.Correcto. Puesto que la entrada f es 1.5 y la salida es 2, y la entrada de g es 1.5, estas dos funciones no son la recíproca de uno a.

Gráficos de lo recíproca de funciones

Lo sentimos, pero la GeoGebra Applet no se pudo iniciar. Por favor, asegúrese de que Java 1.4.2 (o posterior) está instalado y activo en su navegador ( Haga clic aquí para instalar Java ahora )
El manipulante 1: Lo recíproca de una función linear.

Cuando las funciones son lo recíproca de uno a, sus gráficos tienen una relación especial. Aquí está el gráfico de y=3x+2 y de su recíproca y=x/3-2/3. Vea que cada punto de cada recta está reflejado a través de la recta y=x a un punto correspondiente en la otra recta.

Chasque encendido el punto púrpura en el manipulante 1 y arrástrelo para cambiar la figura. Note que como usted mueve el punto a lo largo de la recta, los coordenadas del punto son lo recíproca de los coordenadas del punto en la función inversa.

Lo sentimos, pero la GeoGebra Applet no se pudo iniciar. Por favor, asegúrese de que Java 1.4.2 (o posterior) está instalado y activo en su navegador ( Haga clic aquí para instalar Java ahora )
El manipulante 2: Dibuje lo recíproca de una función.
 Chasque encendido el punto azul en el manipulante 2 y arrástrelo para dibujar lo recíproca de la función en el manipulante. Para cambiar la función, primero mueva el punto azul tan cerca al centro de la ventana como sea posible. Entonces la derecha - chasque encendido la recta azul que representa la función. En el menú drop-down, chasque encendido “redefinen�. Entonces mecanografíe adentro la función en la caja de texto. Usted debe comenzar la función con el “y=� y utilizar x como la variable independiente. Utilice el ^ para los exponentes.

Encontrar lo recíproca de una ecuación linear

Pasos para conseguir lo recíproca de una ecuación linear
PasoResultadoJustificación
1f(x)=2x-1Ecuación cuyo encontrar lo recíproca.
2y=2x-1Cambie f(x) al y.
3y+1=2x-1+1Agregue 1 a ambos lados.
4y+1=2xSimplifique.
5(y+1)/2=2x/2Divida ambos lados por 2.
6y/2+1/2=xSimplifique.
7y=x/2+1/2Intercambie las variables.
8f-1(x)=x/2+1/2Cambie de nuevo a la notación de la función.

Citar este artículo como:
Función recíproca. 2009-04-03. Enciclopedia de Todas las Palabras de la Matemáticas. Life is a Story Problem.org. http://www.allmathwords.org/es/i/inverseofafunction.html.

Traducciones

créditos de imagen

  • Todas las imágenes y manipulatives están por David McAdams a menos que estén indicadas de otra manera. Todas las imágenes de David McAdams son & de los derechos reservados; © Life is a Story Problem.org y se puede reproducir para el uso educativo no comercial solamente.

La historia de revisión


2009-04-03: Traducido automáticamente por BabelFish. (babelfish.yahoo.com.)
2008-09-19: Cuadro agregado 1, 1 manipulante, y 2 manipulantes (McAdams, David.)
2008-08-13: Agregado '' más información '' y números de paso corregidos en '' encontrar lo contrario de una función linear '' (McAdams, David.)
2008-04-05: Énfasis agregado del color. Cheque agregado de la comprensión (McAdams, David.)
2007-07-12: Versión inicial (McAdams, David.)

Enciclopedia de Todas las Palabras de la Matemáticas es un servicio de Life is a Story Problem.org.
Los derechos reservados ©2005-2009 de Life is a Story Problem.org. Todos los derechos reservados.
Creative Commons License Este trabajo se autoriza debajo de una Creative Commons Attribution-Noncommercial-Share Alike 3.0 License