Raíz múltiple
|
Una raíz múltiple de un
polinomio
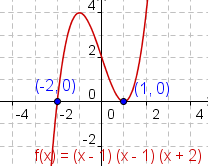
es una raíz que ocurre más de una vez. Tome el polinomio en el cuadro 1
El cuadro 2 demuestra el gráfico del polinomio
|
|
Descubrimiento
|
El manipulante 1 le deja cambiar la multiplicidad de las raíces del polinomio
|
Citar este artículo como:
Raíz múltiple. 2009-04-03. Enciclopedia de Todas las Palabras de la Matemáticas. Life is a Story Problem.org. http://www.allmathwords.org/es/m/multipleroot.html.
Traducciones
créditos de imagen
- Todas las imágenes y manipulatives están por David McAdams a menos que estén indicadas de otra manera. Todas las imágenes de David McAdams son & de los derechos reservados; © Life is a Story Problem.org y se puede reproducir para el uso educativo no comercial solamente.
La historia de revisión
2009-04-03: Traducido automáticamente por BabelFish. (babelfish.yahoo.com.)
2008-12-16: Versión inicial (McAdams, David.)
- Navegación
- Home
- Contenido
-
# A B C D E F G H I J L M N O P Q R S T U V X Y - Ayudas del profesor
- Demostraciones de la Clase
- Referencia recíproca
- Geometría de NYSDE
- LIASP
- LIASP Home
- Condiciones del uso
- Política de aislamiento
- Done a LIASP
- Estructura de la ayuda este sitio
- Sobre LIASP
- LIASP del Contacto
Enciclopedia de Todas las Palabras de la Matemáticas es un servicio de
Life is a Story Problem.org.
Los derechos reservados ©2005-2009 de Life is a Story Problem.org. Todos los derechos reservados.
 Este trabajo
se autoriza debajo de una
Creative Commons Attribution-Noncommercial-Share Alike 3.0 License
Este trabajo
se autoriza debajo de una
Creative Commons Attribution-Noncommercial-Share Alike 3.0 License
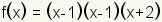 .
El factor
.
El factor
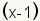 ocurre dos veces, así que es una raíz múltiple. Puesto que ocurre dos veces, también
se llama una
ocurre dos veces, así que es una raíz múltiple. Puesto que ocurre dos veces, también
se llama una 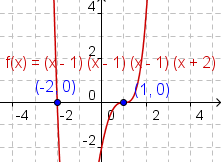
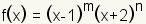 .
Chasque encendido los puntos verdes y azules en los resbaladores y
arrástrelos para cambiar la multiplicidad.
.
Chasque encendido los puntos verdes y azules en los resbaladores y
arrástrelos para cambiar la multiplicidad.