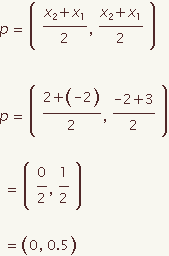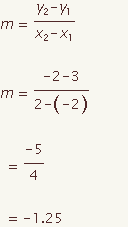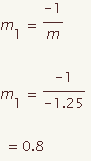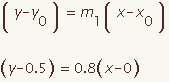Bisectriz perpendicular
|
Un bisectriz perpendicular es una
recta
que biseca
una recta segmento y es
perpendicular
a la recta segmento. En el manipulante 1, la recta segmento AB es la recta segmento
que es bisecado. La recta roja es el perpendicular bisectriz. El punto C
es el punto medio de la recta segmento AB. Chasque encendido los puntos
azules en el manipulante 1 y arrástrelos para cambiar la figura. Para reajustar
el 1 manipulante de nuevo a su configuración original, chasque encendido el botón
de reajuste ( |
Características de un perpendicular bisectriz
|
Cada punto en un bisectriz perpendicular es la misma distancia de las puntos finales. Puesto que todos los puntos en un circunferencia son la misma distancia del centro del circunferencia, dos circunferencias de los mismos tamaños se pueden utilizar para encontrar un perpendicular bisectriz. En el manipulante 2, el punto D es la misma distancia del centro de cada uno de los circunferencias, significando el AD ≡ BD. Mientras que el radio del AD cambia, los puntos D y E están siempre en el perpendicular bisectriz. Chasque encendido el punto D y arrástrelo para remontar el perpendicular bisectriz. Los bisectors perpendiculares de los lados de un triángulo se encuentran en el circuncentro del triángulo. |
|
Los bisectors perpendiculares de los lados de un triángulo se intersecan en un punto llamado el circuncentro del triángulo. |
Construyendo un perpendicular bisectriz
El cuadro 1 demuestra los pasos para crear un perpendicular bisectriz usando un borde recto y un compás. Chasque encendido los puntos azules en cada uno de los manipulatives y arrástrelos para cambiar la figura.
| Paso | Manipulante | Descripción | Justificación |
|---|---|---|---|
 |
La recta segmento AB es la recta segmento a bisecar. | Éstos son los criterios. | |
| 1 | Dibuje un circunferencia con el centro A y el radio AB. | Postulado 3 del libro 1 de los elementos de Euclid: Un circunferencia puede ser drenaje con cualquier centro y cualquier radio. | |
| 2 | Dibuje un circunferencia con el centro B y VAGOS del radio. | Postulado 3 del libro 1 de los elementos de Euclid: Un circunferencia puede ser drenaje con cualquier centro y cualquier radio. | |
| 3 | Marque las intersecciones de los circunferencias como puntos C y D. | Una intersección es un punto de la concurrencia. | |
| 4 | Dibuje una recta a través de los puntos C y D. Esta recta es el perpendicular bisectriz. | Euclid. Postulado 1. del libro 1 de los elementos. Una recta se puede extraer de cualquier punto a cualquier punto. | |
| 5 | La intersección de la recta segmento AB y de la recta CD del segmento es el punto medio de la recta segmento AB | Una intersección es un punto de la concurrencia. | |
| Cuadro 1: Construyendo un perpendicular bisectriz. | |||
Ecuación de un perpendicular bisectriz
|
La ecuación de un bisectriz perpendicular se puede calcular para una recta segmento dada con los puntos del extremo (x1, y1) y (x2, y2). Esta demostración demostrará cómo calcular la ecuación de un perpendicular bisectriz en forma de la pendiente y el punto. Chasque encendido los puntos en 2 manipulantes y arrástrelos para cambiar la figura.
| ||||||||||||||||||||
Más información
- Dendane, A. Bisectriz perpendicular. Analyze Math. 2009-04-03. Traducido automáticamente por babelfish.yahoo.com. http://www.analyzemath.com/Geometry/PerpendicularBisector/PerpendicularBisector.html.
Citar este artículo como:
Bisectriz perpendicular. 2009-04-03. Enciclopedia de Todas las Palabras de la Matemáticas. Life is a Story Problem.org. http://www.allmathwords.org/es/p/perpendicularbisector.html.
Traducciones
créditos de imagen
- Todas las imágenes y manipulatives están por David McAdams a menos que estén indicadas de otra manera. Todas las imágenes de David McAdams son & de los derechos reservados; © Life is a Story Problem.org y se puede reproducir para el uso educativo no comercial solamente.
La historia de revisión
2009-04-03: Traducido automáticamente por BabelFish. (babelfish.yahoo.com.)
2008-11-15: Versión inicial (McAdams, David.)
- Navegación
- Home
- Contenido
-
# A B C D E F G H I J L M N O P Q R S T U V X Y - Ayudas del profesor
- Demostraciones de la Clase
- Referencia recíproca
- Geometría de NYSDE
- LIASP
- LIASP Home
- Condiciones del uso
- Política de aislamiento
- Done a LIASP
- Estructura de la ayuda este sitio
- Sobre LIASP
- LIASP del Contacto
Enciclopedia de Todas las Palabras de la Matemáticas es un servicio de
Life is a Story Problem.org.
Los derechos reservados ©2005-2009 de Life is a Story Problem.org. Todos los derechos reservados.
 Este trabajo
se autoriza debajo de una
Creative Commons Attribution-Noncommercial-Share Alike 3.0 License
Este trabajo
se autoriza debajo de una
Creative Commons Attribution-Noncommercial-Share Alike 3.0 License
 )
en el manipulante.
)
en el manipulante.