Teorema racional de las raíces

El teorema racional de las raíces da raíces racionales posibles de un solo polinomio variable con coeficientes del número entero. Las raíces racionales son una raíz de un polinomio que sea un número racional. Dado un polinomio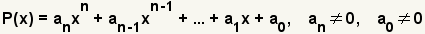 cualquier raíz racional del polinomio tiene un factor de a₀ como numerador y un factor de como denominador. El teorema racional de las raíces también se llama el teorema racional de los ceros.

Comience con el polinómico 2x³ + 5x² - 4x - 3. Desde a₀ = -3, el numerador de cualquier raíz racional debe ser uno de ±1, ±3. Desde a₃ = 2, el denominador de cualquier raíz racional debe ser uno de ±1, ±2.

Para ver porqué, comience con los dos factores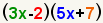 La determinación de cada factor a 0 da las raíces del polinomio: y Las raíces del polinomio (3x+2)(5x-7) son x = 2/3 y x = -7/5.

Ahora multiplique los dos factores del polinomio. Según el teorema racional de las raíces, cualquier raíz racional del polinomio será un factor de -14 dividido por un factor de 15. Los factores de -14 son ±1, ±2, ±7, ±14. Los factores de 15 son ±1, ±3, ±5, ±15.

Ejemplos

Paso	Ecuación	Descripción
1		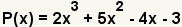Éste es el polinomio cuyo encontrar raíces.
2		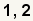Encuentre todos los factores de a0.
3		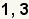Encuentre todos los factores de a3.
4		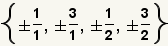Calcule todas las raíces racionales posibles dividiendo los factores de -3 por los factores de 2.
5		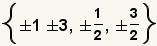Simplifique cualquier fracción que pueda ser simplificada.
6		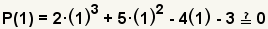Pruebe la raíz x=1 substituye 1 por x.
7		Simplifique los exponentes.
8		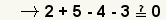Simplifique la multiplicación.
9		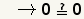Simplifique la suma. Puesto que 0=0 es una declaración verdadera, 1 es una raíz de P(x).
10		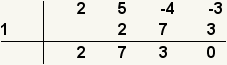Utilice la división sintética para encontrar el factor restante.
11		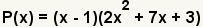Aquí están los factores del polinomio. Utilice la ecuación cuadrático para encontrar cualquier raíz cuadrático del 2x2+7x+3.
Ejemplo 1

Paso	Ecuación	Descripción
1		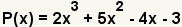Éste es el polinomio cuyo encontrar raíces.
2		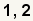Encuentre todos los factores de.
3		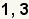Encuentre todos los factores de a0.
4		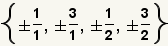Calcule todas las raíces racionales posibles dividiendo los factores de -3 por los factores de 2.
5		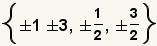Simplifique cualquier fracción que pueda ser simplificada.
6		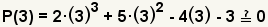Pruebe la raíz x=3 por 3 que substituyen adentro para el X.
7		Simplifique los exponentes.
8		Simplifique la multiplicación.
9		Simplifique la suma y la resta. Desde 84≠0, 3 no es una raíz de P(x).
Ejemplo 2

Citar este artículo como:

Teorema racional de las raíces. 2009-04-03. Enciclopedia de Todas las Palabras de la Matemáticas. Life is a Story Problem.org. http://www.allmathwords.org/es/r/rationalrootstheorem.html.

Traducciones

• Click here to see this article in English.

créditos de imagen

• Todas las imágenes y manipulatives están por David McAdams a menos que estén indicadas de otra manera. Todas las imágenes de David McAdams son & de los derechos reservados; © Life is a Story Problem.org y se puede reproducir para el uso educativo no comercial solamente.

La historia de revisión

2009-04-03: Traducido automáticamente por BabelFish. (babelfish.yahoo.com.)
2009-02-06: Acoplamientos agregados del vocabulario (McAdams, David.)
2009-01-29: Versión inicial (McAdams, David.)