NÚmero real
Un nÚmero real es un nÚmero que se puede encontrar en la recta numÃĐrica real. Al principio, esto puede parecer una manera tonta de definir un nÚmero real. Pero, cuando usted mira en ella, usted puede ver porquÃĐ esto tiene sentido.
Primero apagado, cualquier nÚmero entero o nÚmero entero es un nÚmero real. Generalmente, utilizamos el nÚmero entero para nuestras hacer tictac-marcas en la Recta numÃĐrica real como en el cuadro 1:
 Cuadro 1: Recta numÃĐrica a partir de la -3 a 3. |
Obviamente, podemos encontrar cualquier nÚmero entero en la Recta numÃĐrica simplemente extendiendo la Recta numÃĐrica suficientemente lejos. ÂŋCÃģmo sobre nÚmeros racionales? Tome el 1/2 por ejemplo. Puede ser encontrado intermedio entre cero y uno segÚn las indicaciones del cuadro 2.
 Cuadro 2: Recta numÃĐrica con el nÚmero el 1/2 marcado. |
Ahora mire los nÚmeros irracionales. Tome
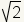 por ejemplo. El valor de
por ejemplo. El valor de 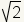 es cerca de 1.41. EstÃĄ tan en la Recta numÃĐrica. VÃĐase el cuadro 3 para este ejemplo.
es cerca de 1.41. EstÃĄ tan en la Recta numÃĐrica. VÃĐase el cuadro 3 para este ejemplo.
 Cuadro 3: Recta numÃĐrica con 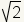 marcado. marcado. |
ÂŋY cÃģmo sobre el nÚmero para el π? ÂĄSÃ! Correcto allà entre 3 y 4 segÚn las indicaciones del cuadro 4.
 Cuadro 4: Recta numÃĐrica con el p marcado. |
ÂŋQuÃĐ nÚmeros no estÃĄn tan en la Recta numÃĐrica real? La respuesta es
nÚmeros complejos.
El diagrama abajo es el plano del nÚmero complejo. Los nÚmeros reales se
pueden encontrar en la Recta numÃĐrica real que es el eje horizontal.
Cualquier otro nÚmero complejo se encuentra en el plano complejo, pero no en
la Recta numÃĐrica real. Hay tres nÚmeros etiquetados en el plano en el cuadro
5. El primer es A(2.0). Puesto que esto estÃĄ en la Recta numÃĐrica
real es un nÚmero real. El segundo es B(0.√2). Ãste es el nÚmero
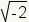 . No estÃĄ en la
Recta numÃĐrica real. El tercero es C(1.1). Ãste es el nÚmero
1+i. No estÃĄ tambiÃĐn en la Recta numÃĐrica real. Tan
. No estÃĄ en la
Recta numÃĐrica real. El tercero es C(1.1). Ãste es el nÚmero
1+i. No estÃĄ tambiÃĐn en la Recta numÃĐrica real. Tan
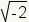 y 1+i
no son los nÚmeros reales.
y 1+i
no son los nÚmeros reales.
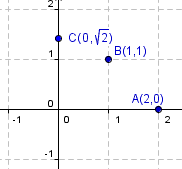 Cuadro 5: El plano complejo. |
Citar este artÃculo como:
NÚmero real. 2009-04-03. Enciclopedia de Todas las Palabras de la MatemÃĄticas. Life is a Story Problem.org. http://www.allmathwords.org/es/r/realnumber.html.
Traducciones
crÃĐditos de imagen
- Todas las imÃĄgenes y manipulatives estÃĄn por David McAdams a menos que estÃĐn indicadas de otra manera. Todas las imÃĄgenes de David McAdams son & de los derechos reservados; © Life is a Story Problem.org y se puede reproducir para el uso educativo no comercial solamente.
La historia de revisiÃģn
2009-04-03: Traducido automÃĄticamente por BabelFish. (babelfish.yahoo.com.)
2008-12-31: Agregado '' mÃĄs informaciÃģn '' (McAdams, David.)
2007-07-12: VersiÃģn inicial (McAdams, David.)
- NavegaciÃģn
- Home
- Contenido
-
# A B C D E F G H I J L M N O P Q R S T U V X Y - Ayudas del profesor
- Demostraciones de la Clase
- Referencia recÃproca
- GeometrÃa de NYSDE
- LIASP
- LIASP Home
- Condiciones del uso
- PolÃtica de aislamiento
- Done a LIASP
- Estructura de la ayuda este sitio
- Sobre LIASP
- LIASP del Contacto
Enciclopedia de Todas las Palabras de la MatemÃĄticas es un servicio de
Life is a Story Problem.org.
Los derechos reservados ÂĐ2005-2009 de Life is a Story Problem.org. Todos los derechos reservados.
 Este trabajo
se autoriza debajo de una
Creative Commons Attribution-Noncommercial-Share Alike 3.0 License
Este trabajo
se autoriza debajo de una
Creative Commons Attribution-Noncommercial-Share Alike 3.0 License