PolûÙgono regular
Un polûÙgono regular es un polûÙgono cuyos lados son longitud igual y cuyos lados son simûˋtricos sobre el centro del polûÙgono. Los polûÙgonos regulares del vario nû¤mero de lados se pueden denotar como ãn-gon regularã?. Un 3-gon regular es tambiûˋn un triûÀngulo equilûÀtero. Un 4-gon regular es tambiûˋn un cuadrado.
| El manipulante 1: PolûÙgonos regulares |
Centro de polûÙgonos regulares
|
Cada polûÙgono regular tiene un centro. Este centro puede ser encontrado construyendo los bisectors perpendiculares de cualquier dos lados del polûÙgono regular. Para los polûÙgonos con un nû¤mero par de lados, puede ser encontrado conectando cualesquiera dos sistemas (enfrente de) de puntos antûÙpodas. El centro de un polûÙgono regular puede ser construido construyendo el bisectriz perpendicular de dos lados. El punto de la intersecciû°n de los bisectriz perpendiculares es el centro del polûÙgono regular. |
û?ngulo central de polûÙgonos regulares
|
El ûÀngulo central de un polûÙgono regular es el ûÀngulo
entre dos semirectas que vayan del centro del polûÙgono regular y pasen con dos
vûˋrtices adyacentes del polûÙgono. La medida del ûÀngulo central de polûÙgonos regulares es
|
Circunferencia circunscrita sobre polûÙgonos regulares
|
Un circunferencia se puede dibujar alrededor de cada polûÙgono regular que intercepte todas las vûˋrtices del polûÙgono y de ninguno de los lados. ûste es el circunferencia circunscrita del polûÙgono regular. El centro del polûÙgono regular es tambiûˋn el centro decircunferencia circunscrita del polûÙgono regular. Chasque encendido los puntos azules enel manipulante 3 y arrûÀstrelos para cambiar la figura. Para construir el circunferencia circunscrita sobre un polûÙgono regular, coloque el punto del compûÀs en el centro del polûÙgono, y la aguja en una vûˋrtice, despuûˋs dibuje el circunferencia. |
Circunferencia inscrita de polûÙgonos regulares
|
Un circunferencia se puede dibujar dentro de cada polûÙgono regular que intercepte cada uno de los lados del polûÙgono exactamente una vez. ûste es el circunferencia inscrita del polûÙgono regular. El centro del polûÙgono regular es tambiûˋn el incentro del polûÙgono regular. Chasque encendido los puntos azules en 3 manipulantes y arrûÀstrelos para cambiar la figura. Para construir el circunferencia inscrita de un polûÙgono regular, construya el punto medio de lados uces de los. Despuûˋs coloque el punto del compûÀs en el centro del polûÙgono, y la aguja en el punto medio, despuûˋs dibuje el circunferencia. |
MûÀs informaciû°n
- McAdams, David E. PolûÙgono. AllMathWords.org. Life is a Story Problem.org. 2009-04-03. http://www.allmathwords.org/article.aspx?lang=es&id=Polygon.
Citar este artûÙculo como:
PolûÙgono regular. 2009-04-03. Enciclopedia de Todas las Palabras de la MatemûÀticas. Life is a Story Problem.org. http://www.allmathwords.org/es/r/regularpolygon.html.
Traducciones
crûˋditos de imagen
- Todas las imûÀgenes y manipulatives estûÀn por David McAdams a menos que estûˋn indicadas de otra manera. Todas las imûÀgenes de David McAdams son & de los derechos reservados; © Life is a Story Problem.org y se puede reproducir para el uso educativo no comercial solamente.
La historia de revisiû°n
2009-04-03: Traducido automûÀticamente por BabelFish. (babelfish.yahoo.com.)
2008-12-31: Ecuaciones cambiadas del HTML a las imûÀgenes (McAdams, David.)
2008-12-11: '' Centro agregado de un polûÙgono regular ''. Figura cambiada del circumcircle a manipulante. '' Incircles agregado de polûÙgonos regulares '' (McAdams, David.)
2008-11-02: Manipulante cambiada a GeoGebra (McAdams, David.)
2008-06-11: Secciû°n agregada en el ûÀngulo central de un polûÙgono regular y de un circumcircle (McAdams, David.)
2008-04-18: Versiû°n inicial (McAdams, David.)
- Navegaciû°n
- Home
- Contenido
-
# A B C D E F G H I J L M N O P Q R S T U V X Y - Ayudas del profesor
- Demostraciones de la Clase
- Referencia recûÙproca
- GeometrûÙa de NYSDE
- LIASP
- LIASP Home
- Condiciones del uso
- PolûÙtica de aislamiento
- Done a LIASP
- Estructura de la ayuda este sitio
- Sobre LIASP
- LIASP del Contacto
Enciclopedia de Todas las Palabras de la MatemûÀticas es un servicio de
Life is a Story Problem.org.
Los derechos reservados ôˋ2005-2009 de Life is a Story Problem.org. Todos los derechos reservados.
 Este trabajo
se autoriza debajo de una
Creative Commons Attribution-Noncommercial-Share Alike 3.0 License
Este trabajo
se autoriza debajo de una
Creative Commons Attribution-Noncommercial-Share Alike 3.0 License
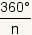 o
o
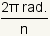 donde estûÀ el nû¤mero n de vûˋrtices del polûÙgono. Chasque encendido los puntos azules
en el manipulante 2 y arrûÀstrelos para cambiar la figura.
donde estûÀ el nû¤mero n de vûˋrtices del polûÙgono. Chasque encendido los puntos azules
en el manipulante 2 y arrûÀstrelos para cambiar la figura.