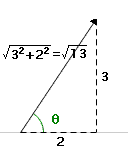Vector
|
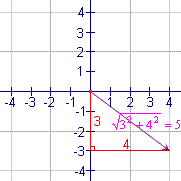
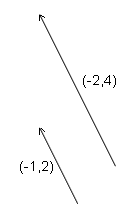
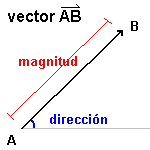
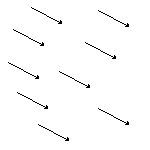
Un vector es un valor que tiene magnitud y dirección. Véase el cuadro 1. La magnitud es representada por la longitud de la recta, y la dirección por la rotación, o el ángulo, de la recta de una dirección de referencia. Por la convención, la dirección de referencia es generalmente el eje horizontal del origen a la derecha. Un vector no tiene una localización. Esto significa que un vector se puede dibujar dondequiera en un gráfico. Cada uno de las representaciones de un vector en el cuadro 2 es el mismo vector. Cada uno de estas representaciones tiene la misma magnitud y dirección asà que son el mismo vector. TÃpicamente, un vector se dibuja con su cola en el origen de un gráfico. Componentes del vectorUn vector de 2 dimensiones se puede también expresar como par ordenado por ejemplo (-3.4). Cada uno de los números se llama un componente. Para el vector (-3, 4), el -3 representa el movimiento o fuerza en la x-dirección, y 4 representa el movimiento en la y-dirección. MagnitudPara obtener la magnitud del vector (x. y),
utiliza la
fórmula de la distancia:
|
|
Ã?ndice del artÃculo
Componentes
Manipulante del vector
vector
Igualdad del vector
Sumar de vector
Multiplicación del vector
 Multiplicación escalar
Multiplicación escalar
 Producto escalar
Producto escalar
Manipulante
|
Chasque encendido los puntos azules etiquetados A y B y arrástrelos para cambiar el manipulante. La flecha roja es el vector. Señale A es el punto de partida del vector. El punto B es el punto de conclusión del vector. Los vectores rayados verdes son el componente horizontal y componente vertical del vector AB. En el cristal de la álgebra a la izquierda, la magnitud es la magnitud del vector AB. Aquà están algunas sugerencias para explorar vectores.
|
Dirección
|
La dirección de un vector se puede expresar como ángulo del eje horizontal. Dado los componentes de un vector, la dirección se puede calcular usando la definición del coseno. Usando el cuadro 4, lechuga romana (?) = 2/v (13) que implican el ? = los arccos (2/v (13)) ˜ 0.9828. |
Igualdad del vector
Dos vectores son iguales si y solamente si todos los componentes correspondientes son iguales.
| Vector 1 | Vector 2 | Igualdad |
|---|---|---|
| (3.4) | (3.4) | Los vectores son igual porque 3 = 3 y 4 = 4. |
| (-3.3) | (3.2) | Los vectores no son iguales porque -3 ≠ 3 y 3 ≠ 2. |
| (-2.1) | (-2.2) | Los vectores no son iguales. Aunque -2 = -2, 1 ≠ 2. |
| (3.-1) | (2.-1) | Los vectores no son iguales. Aunque -1 = -1, 3 ≠ 2. |
Sumar de vector
|
Al agregar vectores, agregue los componentes
correspondientes.
Por ejemplo:
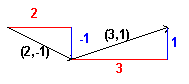
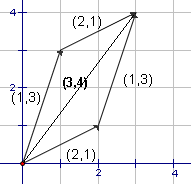
Al representar la suma de vector gráficamente, dibuje la cola de un vector en el mismo lugar como el jefe del otro (véase el cuadro 4). Cuando agregamos los números, no importa que nos numeran agregan primero, 1 + 2 = 2 + 1 = 3. Es igual con vectores. El cuadro 5 demuestra la suma de los vectores (2.1) y (1.3). No hay materia cuál aplicamos primero, el resultado siempre (3.4). La resta del vector se hace la misma manera que la suma. Sin embargo, al restar vectores, importa que viene primero. |
|
Multiplicación del vector
Hay tres tipos de multiplicación del vector se definen que: multiplicación escalar, el producto escalar y el producto vectorial. El producto escalar y el producto vectorial están fuera del alcance de esta enciclopedia. Vea Más información para más información sobre el producto escalar y el producto vectorial.
Multiplicación escalar
|
La multiplicación escalar de vectores consiste
en el multiplicar de un vector por un número. Por ejemplo, la declaración
3 · (-1.-2) está multiplicando el vector (-1.-2)
por el número 3. En la multiplicación escalar, cada componente del
vector es multiplicado por el número. Asà pues, 3
· (-1, -2) =
(3·-1.3·-2)
= (-3.-6).
Note en el cuadro 6, esa multiplicación escalar no cambia la dirección
del vector. Cambia la longitud del vector. Al multiplicar un vector por 2,
el vector resultante será dos veces tan largo.
|
Más información
- vector. buscon.rae.es. REAL ACADEMIA ESPAÑOLA. 2009-05-19. http://buscon.rae.es/draeI/SrvltConsulta?TIPO_BUS=3&LEMA=vector.
Citar este artÃculo como:
Vector. 2009-04-03. Enciclopedia de Todas las Palabras de la Matemáticas. Life is a Story Problem.org. http://www.allmathwords.org/es/v/vector.html.
Traducciones
créditos de imagen
- Todas las imágenes y manipulatives están por David McAdams a menos que estén indicadas de otra manera. Todas las imágenes de David McAdams son & de los derechos reservados; © Life is a Story Problem.org y se puede reproducir para el uso educativo no comercial solamente.
La historia de revisión
2009-04-03: Traducido automáticamente por BabelFish. (babelfish.yahoo.com.)
2008-09-16: Manipulante agregada (McAdams, David.)
2008-04-04: ArtÃculo ampliado (McAdams, David.)
2008-03-11: Referencia agregada a los acoplamientos calientes de la localización y del vocabulario (McAdams, David.)
2007-07-12: Versión inicial (McAdams, David.)
- Navegación
- Home
- Contenido
-
# A B C D E F G H I J L M N O P Q R S T U V X Y - Ayudas del profesor
- Demostraciones de la Clase
- Referencia recÃproca
- GeometrÃa de NYSDE
- LIASP
- LIASP Home
- Condiciones del uso
- PolÃtica de aislamiento
- Done a LIASP
- Estructura de la ayuda este sitio
- Sobre LIASP
- LIASP del Contacto
Enciclopedia de Todas las Palabras de la Matemáticas es un servicio de
Life is a Story Problem.org.
Los derechos reservados ©2005-2009 de Life is a Story Problem.org. Todos los derechos reservados.
 Este trabajo
se autoriza debajo de una
Creative Commons Attribution-Noncommercial-Share Alike 3.0 License
Este trabajo
se autoriza debajo de una
Creative Commons Attribution-Noncommercial-Share Alike 3.0 License
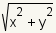 . Para
el vector
. Para
el vector