Exclusive Or

Pronunciation: /ɪkˈsklusɪv ɔr/ Explain

Exclusive or is a logical operation that returns true only if one operand is true and the other is false. For propositions a and b, exclusive or is true if either a or b are true, but not both. Table 1 is the truth table for exclusive or. Exclusive or can also be called an exclusive disjunction. When writing, the term 'exclusive or' is sometimes abbreviated as 'xor'; which is pronounced 'ex-or'.

Three ways in which exclusive or can be written are: a XOR b, a ≠ b, or a ⊕ b. In many programming languages, exclusive or is denoted with the caret symbol (^). In electronics, an exclusive or gate is drawn as: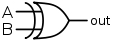

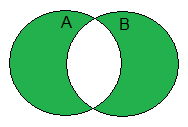
Figure 1: Venn diagram of A xor B.

Properties of Exclusive Or

Property Using Words	Property Using Symbols	Description
a xor false = a	a ⊕ false = a
a xor true = not a	a ⊕ true = ¬a
a xor a = false	a ⊕ a = false	The definition of exclusive or implies that if both operands are true, or both operands are false, then exclusive or returns false. a ≠ a, a xor a must always be false.
a xor not a = true	a ⊕ ¬ a = true	The definition of exclusive or states that if the two operands are not equal, exclusive or returns true. Since a ≠ ¬ a, a xor not a is always true.
a xor b = b xor a	a ⊕ b = b ⊕ a	Exclusive or is commutative.
a xor (b xor c) = (a xor b) xor c	a ⊕ (b ⊕ c) = (a⊕b)⊕ c	Exclusive or is associative.
a xor b = not a xor not b	a ⊕ b = ¬ a ⊕ ¬ b	If the truth value of both operands are swapped, exclusive or still returns the same value.
not (a xor b) = not a xor b = a xor not b	¬(a ⊕ b) = ¬a ⊕ b = a ⊕ ¬b	The logical negation of exclusive or result is the same thing as negating one of the operands of the exclusive or.
a xor b = (a and not b) or (not a and b)	a ⊕ b = (a ∧ ¬b) ∨ (¬a ∧ b)	This is a restatement of the definition of exclusive or: an exclusive or operation is true only if one of the arguments is true and the other is false.
a xor b = (a or b) and (not a or not b)	a ⊕ b = (a ∨ b) ∧ (¬a ∨ ¬b)	This is again a restatement of the definition of exclusive or. The first term (a or b) is true if either a or b is true. The second term (not a or not b) is true if either a and b is false. With the conjunction, the entire expression is true if either a or b are true.
a xor b = (a or b) and not (a and b)	a ⊕ b = (a ∨ b) ∧ ¬(a ∧ b)	This is another restatement of the definition of exclusive or.
Table 2: Properties of Exclusive Or.

Bitwise Exclusive Or

In logic, the operands of exclusive or must be a truth value, must be either true of false. In computers, the operands of exclusive or are binary numbers. The exclusive or is applied to corresponding bits of the operands:
0 xor 0 = 0
0 xor 1 = 1
1 xor 0 = 1
1 xor 1 = 0
1001 xor 1100 = 0101

References

1. McAdams, David E.. All Math Words Dictionary, exclusive or. 2nd Classroom edition 20150108-4799968. pg 75. Life is a Story Problem LLC. January 8, 2015. Buy the book
2. xor. merriam-webster.com. Encyclopedia Britannica. Merriam-Webster. Last Accessed 7/9/2018. http://www.merriam-webster.com/dictionary/XOR?db=luna. Buy the book
3. Boole, George; von Kuffner, Moriz. The mathematical analysis of logic : being an essay towards a calculus of deductive reasoning. pp 52-59. www.archive.org. Macmillan, Barclay, & Macmillan. 1847. Last Accessed 7/9/2018. http://www.archive.org/stream/mathematicalanal00booluoft#page/52/mode/1up/search/exclusive. Buy the book

Cite this article as:

McAdams, David E. Exclusive Or. 4/20/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. http://www.allmathwords.org/en/e/exclusiveor.html.

Image Credits

• All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.

Revision History

4/20/2019: Updated expressions and equations to match new format. (McAdams, David E.)
12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
7/5/2018: Removed broken links, updated license, implemented new markup, implemented new Geogebra protocol. (McAdams, David E.)
2/1/2010: Added "References". (McAdams, David E.)
4/18/2009: Corrected discussion of a xor a. (McAdams, David E.)
1/8/2009: Initial version. (McAdams, David E.)