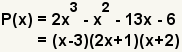Factoring Polynomials

Pronunciation: /ˈfæk.tər.ɪŋ ˌpɒl.əˈnoʊ.mi.əlz/ Explain

P(x)=2x^3-x^2-13x-6=(x-3)(2x=1)(x+2)
Figure 1: A factored polynomial.

To factor a polynomial is to find two or more factors of a polynomial. The factors of a polynomial are a set of polynomials of lesser or equal degree that, when multiplied together, make the original polynomial. To factor a polynomial completely is to find the factors of least degree that, when multiplied together, make the original polynomial.

Stated mathematically, to factor a polynomial P(x), is to find two or more polynomials, say Q(x) and R(x), of lesser degree such that P(x) = Q(x) · R(x). In example 1, x - 3, 2x + 1, and (x + 2) are factors of the polynomial 2x3 - x2 - 13x - 6.

Factoring Step 1: Factor Out the Greatest Common Factor

To factor a polynomial, first find the greatest common factor of the terms. The greatest common factor can be found by:

  1. Finding the prime factorization of each of the terms.
  2. Identifying the common factors.
  3. Multiplying the common factors together to get the greatest common factor.

StepFigureDescription
1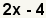2x-4 This is the polynomial to factor.
2Find the greatest common factor of the terms.
2.12x=2*x, -4=-2*2 Find the prime factorization of the terms. The prime factors of 2x are 2 and x. The prime factors of 4 are 2 and 2. The -1 is used to preserve the sign. Since the value of x is unknown, for the purposes of factoring, it is taken to be prime.
2.22x=2*x, -4=-2*2 with the factors '2' highlighted. Identify the common factors. In this case, 2 is the only common factor.
2.3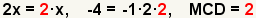2x=2*x, -4=-2*2, GCF=2, with the '2' highlighted. Calculate the greatest common factor (GCF). Since the only common factor is 2, the greatest common factor must also be 2.
3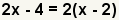2x-4 = 2(2x-2) Rewrite the polynomial as the greatest common factor multiplied by each of the terms with the greatest common factor removed.
42(2x-2)=2*2x-2*2=4x-4 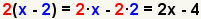Check the work by multiplying the polynomials using the distributive property of multiplication.
Example 1

StepFigureDescription
1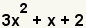3x^2+x+2 This is the polynomial to factor.
2Find the greatest common factor of the terms.
2.1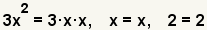3x^2=3*x*x, x=x, 2=2. Find the prime factorization of the terms. The prime factors of 3x2 are 3 · x · x. The prime factor of x is x. The prime factor of 2 is 2. Since the value of x is unknown, for the purposes of factoring, it is taken to be prime.
2.23x^2=3*x*x, x=x, 2=2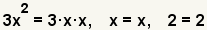. Identify the common factors. In this case, 1 is the only common factor. Since a factor of 1 is not useful, this step is done.
Example 2

StepFigureDescription
1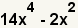14x^4-2x^2 This is the polynomial to factor.
2Find the greatest common factor of the terms.
2.1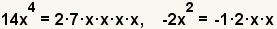14x^4=2*7*x*x*x*x, -2x^2=-1*2*x*x Find the prime factorization of the terms. The prime factors of 14x4 are 2 · 7 · x · x · x · x. The prime factors of 2x2 are 2 · x · x. The -1 is used to preserve the sign. Since the value of x is unknown, for the purposes of factoring, it is taken to be prime.
2.2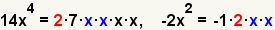14x^4=2*7*x*x*x*x, -2x^2=-1*2*x*x with the factors '2' highlighted and two factors 'x' highlighted. Identify the common factors. In this case, 2, x and x are the common prime factors.
2.3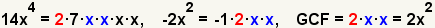14x^4=2*7*x*x*x*x, -2x^2=-1*2*x*x, GCF=2*x*x=2x^2 with the factors '2' highlighted and two factors 'x' highlighted. Calculate the greatest common factor (GCF). Since the common prime factors are 2, x and x, the greatest common factor is 2 · x · x = 2x2.
3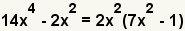14x^4-2x^2 = 2x^2(7x^2-1) Rewrite the polynomial as the greatest common factor multiplied by each of the terms with the greatest common factor removed.
4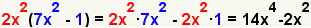2x^2(7x^2-1)=2x^2*7x^2+2x^2*(-1)=14x^4-2x^2 Check the work by multiplying the polynomials using the distributive property of multiplication.
Example 3

Factoring Polynomials of Degree 2 Using the Quadratic Formula

The second step in factoring a degree 2 polynomial, also called a quadratic equation, is to determine if it can be factored using real numbers. The discriminant of a degree 2 polynomial tells how many and what types of solutions can be found for a quadratic equation. For a quadratic equation f(x) = ax2 + bx + c, the discriminant is b2 - 4ac.

DiscriminantSolutionsExample
b2 - 4ac < 0 Two complex solutions; No real solutions.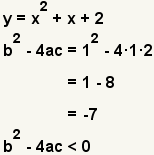y=x^2+x+2,b^2-4ac=1^1-4*1*2=1-8=-7, b^2-4ac<0
b2 - 4ac = 0 One real solution. 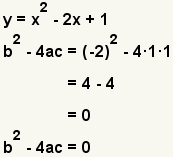y=x^2-2x+1,b^2-4ac=(-2)^1-4*1*1=4-4=0, b^2-4ac=0
b2 - 4ac > 0 Two real solutions.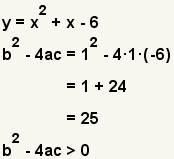y=x^2+x-6,b^2-4ac=1^1-4*1*(-6)=1+24=25, b^2-4ac>0
Table 1: Discriminant and solutions of a quadratic equation

If the are no real solutions, the quadratic can not be factored further without using complex numbers. If there are real solutions, use the quadratic function to find the solutions.

Factoring a Quadratic With Two Real Solutions

EquationDescription
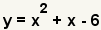y=x^2+x-6 This is the equation to factor.
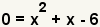0=x^2+x-6 Since we are finding the roots of the polynomial, set y to 0.
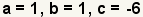a=1, b=1, c=-6 Identify a, b, and c in the quadratic function. a = 1 and b = 1 since the implied coefficient of x2 and x are 1.
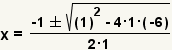x=(-1+-square root(1^2-4*1*(-6)))/(2*1)Fill in the quadratic formula.
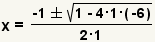x=(-1+-square root(1-4*1*(-6)))/(2*1)Simplify the exponent.
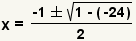x=(-1+-square root(1-(-24)))/2Simplify multiplication.
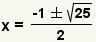x=(-1+-square root(25))/2Simplify addition and subtraction.
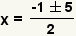x=(-1+-5)/2Simplify the square root.
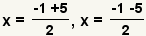x=(-1+5)/2, x=(-1-5)/2Split the solution into two explicit equations.
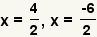x=4/2, x=-6/2Simplify the numerators.
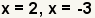x=2, x=-3Simplify the fractions.
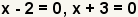x-2=0, x+3=0Get zero on one side of the equation to make the factors.
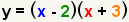y=(x-2)(x+3)Rewrite the equation using the factors.
y=x*x+x*3+x*(-2)+(-2)(3)Check the work. Use the FOIL method to multiply out the factors.
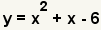y=x^2+x-6Simplify the terms and add like terms. This is the original equation, so the factoring is correct.
Example 4.

Factoring a Quadratic With One Real Solution

EquationDescription
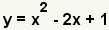y=x^2-2x+1This is the equation to factor.
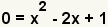0=x^2-2x+1Since we are finding the roots of the polynomial, set y to 0.
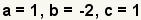a=1, b=-2, c=1Identify a, b, and c in the quadratic function. a = 1 since the implied coefficient of x2 is 1.
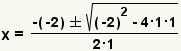x=(-(-2)+-square root((-2)^2-4*1*1))/(2*1)Fill in the quadratic formula.
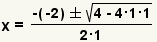x=(2+-square root(4-4*1*1))/(2*1)Simplify the exponent.
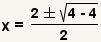x=(2+-square root(4-4))/2Simplify multiplication.
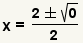x=(2+-square root(0))/2Simplify addition and subtraction.
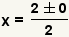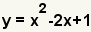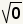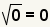x=(2+-0)/2Since Square root of -7 equals square root of (7)i., substitute square root(7)i for Square root of (-7)..
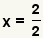x=2/2Since anything plus zero is itself and anything minus zero is itself, the plus or minus zero goes away.
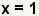x=1Reduce the fraction.
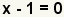y=(x-1)(x-1)Subtract 1 from both sides to get the factor.
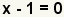y=(x-1)(x-1)Write out the factors. Since there is only one root of the polynomial, it is a double root.
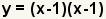y=x*x-1x-1x+1Check the work. Use the FOIL method to multiply out the factors.
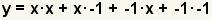y=x^2-2x+1Simplify the terms and add like terms. This is the original equation, so the factoring is correct.
Example 5.

Factoring a Quadratic With No Real Solutions

If the range of the equation is limited to real numbers, a quadratic with no real solutions can not be factored any further. Example 4 shows how to solve a quadratic equation with no real solutions.

EquationDescription
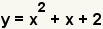y=x^2+x+2This is the equation to factor.
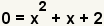0=x^2+x+2Since we are finding the roots of the polynomial, set y to 0.
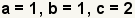a=1, b=1, c=2Identify a, b, and c in the quadratic function. a = 1 and b = 1 since the implied coefficients x are 1.
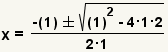x=(-1+-square root(1^2-4*1*2))/(2*1)Fill in the quadratic formula.
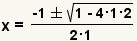x=(-1+-square root(1-4*1*2))/(2*1)Simplify the exponent.
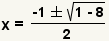x=(-1+-square root(1-8))/2Simplify multiplication.
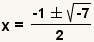x=(-1+-square root(-7))/2Simplify addition and subtraction.
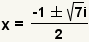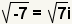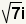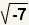x=(-1+-square root(7)i)/2Since Square root of -7 equals square root(7)i., substitute square root(7)i for Square root of -7x..
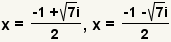x=(-1+square root(7)i)/2, x=(-1-square root(7)i)/2Split the solution into two explicit equations.
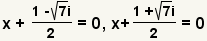x+(1-square root(7)i)/2)=0, x+(1+square root(7)i)/2)=0Get 0 on one side of the equation to get the factors.
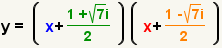y=(x+(1-square root(7)i)/2))(x+(1+square root(7)i)/2)=0)Rewrite the equation using the factors.
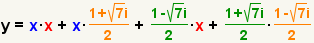y=x*x-1x-1x+1Check the work. Use the FOIL method to multiply out the factors.
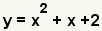y=x^2-2x+1Simplify the terms and add like terms. This is the original equation, so the factoring is correct.
Example 6.

Factoring Polynomials With Degree 3 or Greater

The formulas for solving polynomials with degree 3 and degree 4 are so complicated, that they are only useful in computer programs. Polynomials of degree 5 and higher can not be solved with a formula. The fundamental theorem of algebra implies that every non-constant polynomial with real coefficients can be factored over the real numbers into a product of linear factors and irreducible quadratic factors. While the fundamental theorem of algebra says the factors exist, it does not tell us how to find them.

There are many methods that can be used to find the factors. The rational roots theorem can be used to find possible roots of a polynomial. Interpolation is another method that can be used to approximate the roots of a polynomial. Graphical solutions can also approximate roots and factors of a polynomial.

References

  1. McAdams, David E.. All Math Words Dictionary, factor. 2nd Classroom edition 20150108-4799968. pg 77. Life is a Story Problem LLC. January 8, 2015. Buy the book
  2. Wells, Webster. Factoring. www.archive.org. D. C. Heath & Co., Publishers. 1902. Last Accessed 7/11/2018. http://www.archive.org/stream/factoring00wellrich#page/26/mode/1up/search/theorem. Buy the book
  3. Albert, A. Adrian. Introduction To Algebraic Theories. pp 1-18. www.archive.org. The University of Chicago Press. 1941. Last Accessed 7/11/2018. http://www.archive.org/stream/introductiontoal033028mbp#page/n13/mode/1up/search/factor+theorem. Buy the book
  4. Bettinger, Alvin K. and Englund, John A.. Algebra and Trigonometry. pp 25-30. www.archive.org. International Textbook Company. January 1963. Last Accessed 7/11/2018. http://www.archive.org/stream/algebraandtrigon033520mbp#page/n18/mode/1up. Buy the book
  5. Barbeau, E.J.. Polynomials. pp 93-104. Springer. October 9, 2003. Last Accessed 7/11/2018. Buy the book

More Information

  • McAdams, David E.. Solving Graphically. allmathwords.org. All Math Words Encyclopedia. Life is a Story Problem LLC. 3/12/2009. http://www.allmathwords.org/en/s/solvinggraphically.html.

Cite this article as:

 McAdams, David E. Factoring Polynomials. 4/21/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. http://www.allmathwords.org/en/f/factoringpolynomials.html.

Image Credits

Revision History

4/21/2019: Modified equations and expression to match the new format. (McAdams, David E.)
12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
7/9/2018: Removed broken links, updated license, implemented new markup, implemented new Geogebra protocol. (McAdams, David E.)
2/4/2010: Added "References". (McAdams, David E.)
5/4/2009: Corrected text for example 2. (McAdams, David E.)
1/20/2009: Initial version. (McAdams, David E.)

All Math Words Encyclopedia is a service of Life is a Story Problem LLC.
Copyright © 2018 Life is a Story Problem LLC. All rights reserved.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License