Distance
Pronunciation: /ˈdɪstəns/ ?Distance is a measure in one dimension. By convention distance is always positive. If one takes a line and marks it off in equally spaced units, one can measure one-dimensionally. A directed distance is a distance that can be positive or negative.
When describing multi-dimensional objects, such as rectangles (2-dimensional) or solids (3-dimensional), length is the measure of the longest dimension.
Width or breadth measure at right angles to the length. Height measures vertically at right angles to both length and width.
| Abbreviation | Unit of Measure for Distance | Equals |
|---|---|---|
| Metric System See also International System of Units. | ||
| - | micrometer | 0.000001 m = 10-6 m |
| mm | millimeter | 0.001 m = 10-3 m |
| cm | centimeter | 0.01 m = 10-2 m |
| - | decimeter | 0.1 m = 10-1 m |
| m | meter | 1 m |
| - | decameter | 10 m = 101 m |
| - | hectometer | 100 m = 102 m |
| km | kilometer | 1000 m = 103 m |
| - | megameter | 1000000 m = 106 m |
| gm | gigameter | 1000000000 m = 109 m |
| English System | ||
| in or " | inch | 1/12 ft ≈ 0.0254m |
| ft or ' | foot | 1 ft ≈ 0.3048m |
| yd | yard | 3 ft ≈ 0.9144m |
| mi | mile | 5280 ft ≈ 1609.344m |
| Table 1: Units of Measure. | ||
Equality of Distance
|
Two points that are the same distance from a reference point are said to be equidistant from each other. When distance is taken to be positive, the distance from point A to point B is the same as the distance from point B to point A. |
|
Calculation of Distance
|
The calculation of the distance from one point to another point uses the distance formula 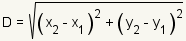 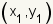 and and
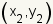 are the coordinates of the
two points. are the coordinates of the
two points.
|
|
The distance from point C to a line AB is defined as the shortest distance from the point to any point on the line. The shortest distance is found by constructing a new line, say CD that passes through point C perpendicular to line AB. So the first thing to do when calculating the distance from a point to a line is find the equation of this line. The slope of the new line CD is equal to the reciprocal of the slope of line AB. You can use the point-slope form of a line to find the equation of the line CD. Once the equation of line CD is found, find the coordinates of the
intersection of line AB and CD, which is point D.
Since the coordinates of D are the solution of the linear system containing
line Once the coordinates of D have been calculated, all that is left
to do is find the distance from C to D. Use the algorithm
for the distance between two points.
|
|
The distance between lines make sense only for lines that are always the same distance apart. This means that the distance between lines only makes sense for parallel lines. The distance from line AB to a line CD is defined as the shortest distance from a point on CD to any point on the line AB. After selecting an arbitrary point on CD, follow the algorithm for finding the distance between a point and a line. |
More Information
- McAdams, David. Directed Distance. allmathwords.org. Life is a Story Problem LLC. 2009-03-12. http://www.allmathwords.org/article.aspx?lang=en&id=Directed%20Distance.
- McAdams, David. Distance Formula. allmathwords.org. Life is a Story Problem LLC. 2009-03-12. http://www.allmathwords.org/article.aspx?lang=en&id=Distance%20Formula.
Cite this article as:
Distance. 2010-03-15. All Math Words Encyclopedia. Life is a Story Problem LLC. http://www.allmathwords.org/en/l/length.html.
Translations
Image Credits
- All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under the Creative Commons Attribution-Noncommercial-Share Alike 3.0 License.
Revision History
2010-03-15: Retitled the article 'Distance'. (McAdams, David.)
2008-12-12: Added calculation of distance. Added 'Distance Formula' to 'More Information' (McAdams, David.)
2008-05-07: Added text about directed distance (McAdams, David.)
2008-04-16: Added 'Units of Measure for Distance' table (McAdams, David.)
2008-04-01: Initial version (McAdams, David.)
- Navigation
- Home
- Contents
-
# A B C D E F G H I J K L M N O P Q R S T U V W X Y Z - Teacher Aids
- Classroom Demos
- Cross Reference
- NYSDE Geometry
- LIASP
- LIASP Home
- Conditions of Use
- Privacy Policy
- Donate to LIASP
- Help build this site
- About LIASP
- Contact LIASP
All Math Words Encyclopedia is a service of
Life is a Story Problem LLC.
Copyright © 2005-2011 Life is a Story Problem LLC. All rights reserved.
 This work is licensed under a Creative Commons Attribution-Noncommercial-Share Alike 3.0 License
This work is licensed under a Creative Commons Attribution-Noncommercial-Share Alike 3.0 License