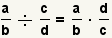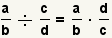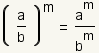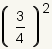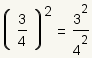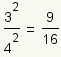Operations on Fractions
Pronunciation: /ˌɒ.pəˈreɪ.ʃənz ɒn ˈfræk.ʃənz/ Explain
An
operation
is something like addition and multiplication. An
operation on a fraction
applies
one of these operations to fractions.
Article Index
How to Add and Subtract Fractions
To add or subtract fractions, one must
first find a common denominator. The
least common denominator
is used since it simplifies the calculations.
Addition Example 1
| Step | Expressions | Description |
|---|
| 1 | 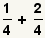 |
These are the fractions to add. |
| 2 | 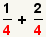 |
Since the denominators are already equal, there
is no need to find a least common denominator. |
| 3 | 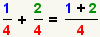 |
Write a new fraction with the addition on top and the common denominator on the
bottom. |
| 4 | 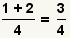 |
Add the numerator. Since the numerator
3 and the denominator 4 are relatively prime, the fraction can not be simplified further. The problem is done. |
| Table 1: Addition of fractions example 1. |
Addition Example 2
| Step | Expressions | Description |
|---|
| 1 | 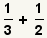 |
These are the fractions to add. |
| 2 | 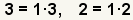 |
The first step in finding the least common denominator is finding the
prime factorization
of each of the denominators. |
| 3 | 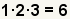 |
Combine the prime factors to get the least common denominator.
6 is the least common denominator. |
| 4 | 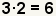 |
Find the number to multiply by the first fraction. Since the least
common denominator is 6, and the denominator
of the first fraction is 3, what times
3 equals 6? |
| 5 | 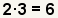 | Find the number to multiply by the
second fraction. Since the least common denominator is
6, and the denominator of the second fraction
is 2, what times 2
equals 6? |
| 6 |  |
We will use the
property of multiplying
by 1 to transform the fractions. |
| 7 | 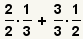 |
Apply the property of multiplying by 1. |
| 8 | 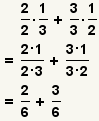 | Multiply the fractions. |
| 9 | 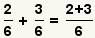 |
Since the denominators are equal, add the numerators. |
| 10 | 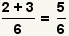 |
Add the numerator. Since the numerator 5 and
the denominator 6 are relatively prime, the
fraction can not be simplified further. The problem is complete. |
| Table 2: Addition of fractions example 2. |
Subtraction Example 1
| Step | Expressions | Description |
|---|
| 1 | 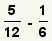 |
These are the fractions to subtract. |
| 2 | 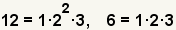 |
The first step in finding the least common denominator is finding the prime
factorization of each of the denominators. |
| 3 | 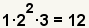 |
Combine the prime factors to get the least common denominator.
12 is the least common denominator. |
| 4 | 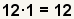 |
Find the number to multiply by the first fraction. Since the least
common denominator is 12, and the denominator
of the first fraction is 12, what times
12 equals 12?
1 times 12 equals 12.
This means that the first fraction already has the least common denominator. |
| 5 | 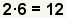 |
Find the number to multiply by the second fraction. Since the least common
denominator is 12, and the denominator of the
second fraction is 6, what times
6 equals 12? |
| 6 | 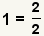 |
We will use the property of multiplying by 1
to transform the fractions. |
| 7 | 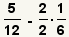 | Apply the property of multiplying by
1. |
| 8 | 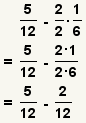 |
Multiply the fraction. |
| 9 | 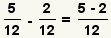 |
Since the denominators are equal, subtract the numerators. |
| 10 | 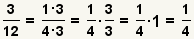 |
The numerator and the denominator are not relatively prime. Find
and cancel the common factor. |
| Table 3: Addition of fractions example 3. |
General Case of Addition
To derive the general case, start with addition of two
arbitrary
fractions:
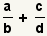
.
The
denominators
are not equal, so the fractions can not yet be added. Since the denominators are
b and
d,
b · d will always be a
common denominator. However,
b ·
d may
not be the least common denominator.
First use the
property of multiplying by 1.
Apply the property of multiplying by
1 to the fraction
to get
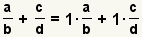
.
But, since
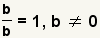
and

,
substitute
b / b and
d / d into the expression, getting
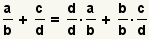
.
Multiply the fractions to get
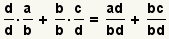
.
Since the denominators are now common, add the numerators:
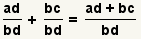
.
We can now conclude

.
How to Multiply Fractions
To multiply fractions, multiply the numerators by each
other and the denominators by each other:
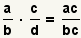
.
Multiplication Example 1
| Step | Expressions | Description |
|---|
| 1 | 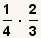 |
These are the fractions to multiply. |
| 2 | 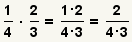 |
Multiply the numerators and the denominators. |
| 3 | 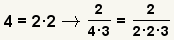 |
Expand the numerator and denominator into prime factors. |
| 4 | 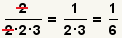 |
Cancel the common factors, then multiply out the numerator and denominator.
Since 1 is prime relative to
6, this fraction can not be reduced any further.
The problem is done. |
| Table 4: Multiplication of fractions example 1. |
Multiplication Example 2
| Step | Expressions | Description |
|---|
| 1 | 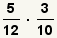 | \
These are the fractions to multiply. |
| 2 | 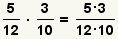 |
Multiply the numerators and the denominators. |
| 3 | 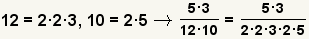 |
Expand the numerator and denominator into factors. |
| 4 | 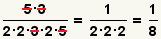 |
Cancel the common factors, then multiply out the numerator and denominator.
Since 1 is prime relative to
8, this fraction can not be reduced any further. The
problem is done. |
| Table 5: Multiplication of fractions example 2. |
How to Divide Fractions
When dividing fractions, use the property of fractions
that dividing by a fraction is the same as multiplying by its reciprocal:
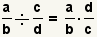
.
Division Example 1
| Step | Expressions | Description |
|---|
| 1 | 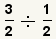 |
These are the fractions to divide. |
| 2 | 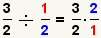 |
Change the division problem into a multiplication problem by flipping the
divisor. |
| 3 | 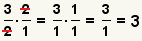 |
Cancel the common factors and simplify the fraction. |
| Table 6: Division of fractions example 1. |
Division Example 2
| Step | Expressions | Description |
|---|
| 1 | 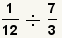 |
These are the fractions to divide. |
| 2 |  |
Change the division problem into a multiplication problem by flipping
the divisor. |
| 3 | 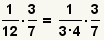 | Find the common factors. |
| 4 | 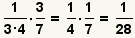 |
Cancel the common factors and simplify the fraction. |
| Table 7: Division of fractions example 2. |
Derivation of the Division Rule for Fractions
| Step | Expressions | Description |
|---|
| 1 | 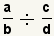 |
Start with a general case of fractions to divide.
a,
b,
c and
d represent
arbitrary values. |
| 2 | 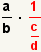 |
The definition of division is 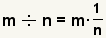 . Use the
definition of division to transform the divisor. . Use the
definition of division to transform the divisor. |
| 3 | 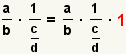 |
This step will use the property of multiplying by 1:
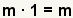 .
Use to property of multiplying by 1 to multiplying
the right side by 1. .
Use to property of multiplying by 1 to multiplying
the right side by 1. |
| 4 | 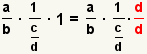 |
This step will use the property of dividing a value by itself:
 . Use the substitution property of
equality to replace the 1 with . Use the substitution property of
equality to replace the 1 with
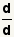 . . |
| 5 | 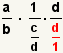 |
Since 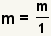 , replace the
d in the denominator of the last
fraction with , replace the
d in the denominator of the last
fraction with 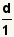 . . |
| 6 | 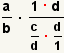 |
Combine the two fractions on the right. |
| 7 | 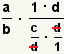 |
Cancel the d's. |
| 8 | 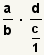 |
Simplify the denominator on the right. |
| 9 | 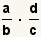 |
Use the fact that 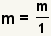 to replace to replace
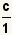 with with  . . |
| 10 | 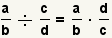 |
We have shown that 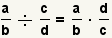 |
| Table 8: Derivation of the division rule for
fractions. |
How to Raise a Fraction to a Power
If a fraction is raised to a power, the numerator and
denominator can each be raised to the same power:
Exponentiation of Fractions Example 1
| Step | Expressions | Description |
|---|
| 1 | 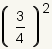 |
This is the fraction to raise to a power. |
| 2 | 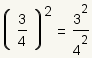 |
Apply the power rule for fractions. |
| 3 | 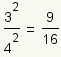 |
Simplify the numerator and denominator. |
| Table 6: Exponentiation of fractions example 1. |
Cite this article as:
McAdams, David E. Operations on Fractions. 4/27/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. http://www.allmathwords.org/en/o/operationsonfractions.html.
Image Credits
Revision History
4/27/2019: Changed equations and expressions to new format. (
McAdams, David E.)
12/21/2018: Reviewed and corrected IPA pronunication. (
McAdams, David E.)
9/5/2018: Removed broken links, updated license, implemented new markup. (
McAdams, David E.)
8/7/2018: Changed vocabulary links to WORDLINK format. (
McAdams, David E.)
1/15/2009: Initial version. (
McAdams, David E.)
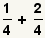
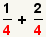
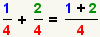
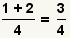
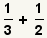
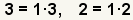
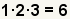
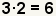
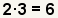

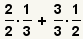
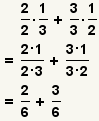
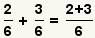
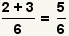
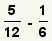
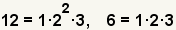
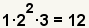
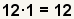
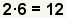
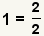
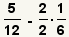
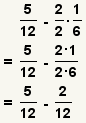
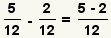
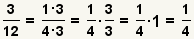
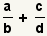 .
.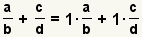 .
.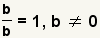 and
and  ,
,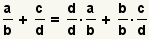 .
.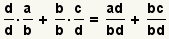 .
.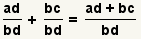 .
. .
.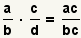 .
.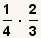
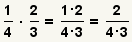
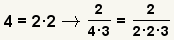
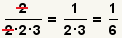
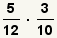
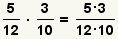
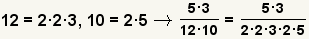
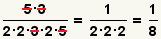
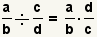 .
.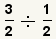

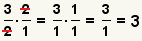
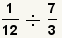

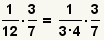
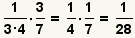
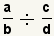
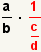
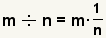 . Use the
definition of division to transform the divisor.
. Use the
definition of division to transform the divisor.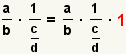
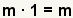 .
Use to property of multiplying by 1 to multiplying
the right side by 1.
.
Use to property of multiplying by 1 to multiplying
the right side by 1.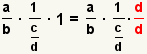
 . Use the substitution property of
equality to replace the 1 with
. Use the substitution property of
equality to replace the 1 with
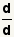 .
.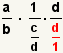
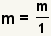 , replace the
d in the denominator of the last
fraction with
, replace the
d in the denominator of the last
fraction with 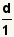 .
.

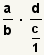
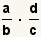
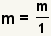 to replace
to replace
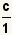 with
with  .
.