Triangle
Pronunciation: /ˈtraɪˌæŋ.gəl/ ExplainA triangle is a three sided polygon[2][3]. All triangles have three non-collinear sides made up of straight line segments. All triangles have three angles.
|
|
| Figure 1: Examples of triangles | Figure 2: Examples of shapes that are not triangles. |
Article Index
Parts of a Triangle
Types of Triangles
 Right Triangle
Right Triangle
 Acute Triangle
Acute Triangle
 Obtuse Triangle
Obtuse Triangle
 Scalene Triangle
Scalene Triangle
 Equilateral Triangle
Equilateral Triangle
 Isosceles Triangle
Isosceles Triangle
Labeling Triangles
Properties of Triangles
 Perimeter of a Triangle
Perimeter of a Triangle
 Angle Sum Theorem
Angle Sum Theorem
 Area of a Triangle
Area of a Triangle
 Heron's Formula for Area of a Triangle
Heron's Formula for Area of a Triangle
 Incircle and Incenter of a Triangle
Incircle and Incenter of a Triangle
 Circumcircle and Circumcenter of a Triangle
Circumcircle and Circumcenter of a Triangle
 Median of a Triangle
Median of a Triangle
 Centroid of a Triangle
Centroid of a Triangle
 Altitude of a Triangle
Altitude of a Triangle
 Orthocenter of a Triangle
Orthocenter of a Triangle
 SAS Congruence
SAS Congruence
 Euclid. Elements, Book 1 Proposition 6: If two sides of a triangle are equal, the angles opposite the equal sides are equal.
Euclid. Elements, Book 1 Proposition 6: If two sides of a triangle are equal, the angles opposite the equal sides are equal.
Centers of a Triangle
Parts of a Triangle
|
A triangle has three angles, three vertices, three sides and three pairs of exterior angles. |
Types of Triangles
| Example | Name Click for more information. | Description |
 |
Right triangle | A triangle with one right angle. |
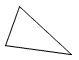 |
Acute triangle | A triangle with three acute angles. |
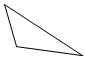 |
Obtuse triangle | A triangle with one obtuse angle. |
 |
Scalene triangle | A triangle whose sides are all different lengths. |
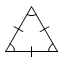 |
Equilateral triangle | A triangle with three equal sides. |
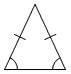 |
Isosceles triangle | A triangle with two equal sides. |
| Figure 3: Types of triangles | ||
Labeling Triangles
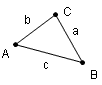
| By convention, triangles are usually labeled in a counterclockwise direction, often using the letters A, B, and C. The sides are often labeled with a lower case letter corresponding to the vertex opposite the side. |
Properties of Triangles
| Perimeter |
|
The perimeter of a triangle is the sides of the triangle or the sum of the lengths of the sides. For example, if the lengths of the sides are 3, 4, and 5, the perimeter is 3 + 4 + 5 = 12. | ||
| Angle Sum Theorem |
| In Euclidean geometry, the sum of the angles of a triangle is 180° = π radians. In other geometries, this might not be true. | ||
| Area |
|
The area of a triangle is
| ||
|
The area of a triangle can also be calculated
from the length of the three sides using Heron's Formula.
First, one must calculate the semiperimeter.
This 1/2 of the
perimeter.
Since the perimeter is a + b +
c where
a, b and
c are the length of the sides of the triangle,
the semiperimeter is 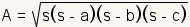 . . | |||
|
Incircle Incenter |
|
The incircle of a triangle is the circle that is tangent to each of the sides of a triangle. The incenter is the center of the incircle. For more information on the incenter of a triangle, see Incenter. | ||
| Circumcircle
Circumcenter |
| The circumcircle of a triangle is the circle that passes through all of the vertices of a triangle. The circumcenter is the center of the circumcircle. For more information on the circumcenter or circumcircle of a triangle, see Circumcenter from All Math Words Encyclopedia. | ||
| Triangle Median Triangle Centroid |
|
A median of a triangle is a line drawn through a vertex of the triangle and the midpoint of the opposite side. This means that every triangle has three medians. The medians of a triangle meet at a point called the centroid of the triangle. The centroid of a triangle is the center of gravity of the triangle. This means that if a triangle is balanced on a pin at the centroid, it would be perfectly balanced. The centroid of a triangle is found by drawing two medians of the triangle[1]. The centroid is at the point where the medians intersect. | ||
| Triangle Altitude |
| An altitude of a triangle is a line segment from a vertex of the triangle to the extended opposite side, perpendicular to the opposite side. | ||
| Triangle Orthocenter |
| The orthocenter of a triangle is at the intersection of the altitudes of a triangle. | ||
| SAS Congruence |
|
Two triangles are congruent if two adjacent sides and the angle contained by the sides are congruent with corresponding sides and angle of the other triangle. In this case we say that the triangles are SAS congruent. SAS stands for side, angle, side. For more information on SAS Congruence, see SAS Congruence. | ||
| Proposition 6, Euclid's Elements: If two angles of a triangle are equal, the sides opposite the equal angles are also equal. |
|
In a triangle, if two angles have equal length, the sides opposite the equal angles are also equal. In figure 16, the angle ABC is equal to the angle ACB. The side AB is also equal to the side AC. For more information on this property of triangles see:
|
Centers of a Triangle
|
Click on the blue points and drag them to change the figure. For what class of triangle are the centroid, orthocenter and circumcenter coincidental? |
| Manipulative 13 - Centers of a Triangle Created with GeoGebra. |
 Understanding Check
Understanding Check
Write your answer on a piece of paper, then use your mouse to click on the 'Click for Answer' text to see the correct answer. Click on the yellow points and drag them to change the manipulative
- For what type of triangle are the five centers shown the same point? Click for Answer Equilateral triangle
- Which centers are always inside a triangle? Click for Answer Centroid and Incenter
- Which centers can be inside or outside a triangle? Click for Answer 9-Point Center, Circumcenter, Orthocenter
- Which center is on the hypotenuse of a right triangle? Click for Answer Circumcenter
- Which center is on the vertex opposite the hypotenuse of a right triangle? Click for Answer Orthocenter
- Which centers are always collinear (on the same line)? Click for Answer 9-Point Center, Centroid, Circumcenter, and the Orthocenter
- For what type of triangle is the orthocenter inside the triangle? Click for Answer Acute Triangle Outside the triangle? Click for Answer Obtuse triangle
References
- McAdams, David E.. All Math Words Dictionary, triangle. 2nd Classroom edition 20150108-4799968. pg 181. Life is a Story Problem LLC. January 8, 2015. Buy the book
More Information
- McAdams, David E.. Angle. allmathwords.org. All Math Words Encyclopedia. Life is a Story Problem LLC. 3/12/2009. http://www.allmathwords.org/en/a/angle.html.
- Euclid of Alexandria. Elements. Clark University. 9/6/2018. https://mathcs.clarku.edu/~djoyce/elements/elements.html.
- Wilson, Jim. Construction of the Nine-Point Circle. jwilson.coe.uga.edu. Jim Wilson's Home Page. University of Georgia. 12/16/2018. http://jwilson.coe.uga.edu/emt668/emt668.folders.f97/anderson/geometry/geometry1project/construction/construction.html.
Cite this article as:
McAdams, David E. Triangle. 5/13/2019. All Math Words Encyclopedia. Life is a Story Problem LLC. http://www.allmathwords.org/en/t/triangle.html.Image Credits
- All images and manipulatives are by David McAdams unless otherwise stated. All images by David McAdams are Copyright © Life is a Story Problem LLC and are licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
Revision History
5/13/2019: Changed equations and expressions to new format. (McAdams, David E.)4/3/2019: Corrected orthocenter manipulative. (McAdams, David E.)
12/21/2018: Reviewed and corrected IPA pronunication. (McAdams, David E.)
12/16/2018: Removed broken links, updated license, implemented new markup. Changed geogebra to new format. (McAdams, David E.)
8/7/2018: Changed vocabulary links to WORDLINK format. (McAdams, David E.)
6/30/2010: Changed 'sum of angles of a triangle' to 'Angle Sum Theorem' in subtitles. (McAdams, David E.)
1/2/2010: Added "References". (McAdams, David E.)
11/28/2009: Added 'Parts of a Triangle'. (McAdams, David E.)
10/30/2008: Changed all manipulatives to GeoGebra. (McAdams, David E.)
9/15/2008: Added wikipedia to more information. (McAdams, David E.)
6/7/2008: Corrected spelling errors. (McAdams, David E.)
3/20/2008: Clarified definition of scalene triangle. (McAdams, David E.)
8/29/2007: Added "Centers of a Triangle". (McAdams, David E.)
8/24/2007: Expanded. (McAdams, David E.)
7/12/2007: Initial version. (McAdams, David E.)
- Navigation
- Home
- Contents
-
# A B C D E F G H I J K L M N O P Q R S T U V W X Y Z - Teacher Aids
- Classroom Demos
- How To
- LIASP
- LIASP Home
- Conditions of Use
- Privacy Policy
- Donate to LIASP
- Help build this site
- About LIASP
- Contact LIASP
All Math Words Encyclopedia is a service of
Life is a Story Problem LLC.
Copyright © 2018 Life is a Story Problem LLC. All rights reserved.
This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License
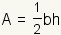 where
where
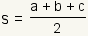 .
.