Número par
Un número
es par si es un número entero y es divisible por 2.
Expresados matemáticamente, incluso los números enteros está en la forma
2k donde está un número entero k. En la notación del conjunto,
incluso los números enteros son
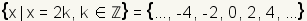 .
.
En el conjunto de numeración decimal, un número entero se puede identificar como par por el hecho de que el dÃgito pasado del número es par. Desde los dÃgitos 0, 2, 4, 6 y 8 son pares, los números 2750, -54, 22, -888 y 1794830495907549234098546 son pares. Un cualquier número entero en la forma decimal que no tiene un dÃgito par pues el dÃgito pasado es impar.
Si un número entero es par o impar se llama paridad. Uno dice, “la paridad de 6 es par,� o “la paridad de -365 es impar.�
Propiedads de números pares
- La suma de dos números enteros pares es también par. Vea la Prueba: La suma de dos números enteros pares es par.
- El producto de dos inúmeros enteros pares es también par. Vea la Prueba: El producto de dos números enteros pares es par.
- La cardinalidad del conjunto de números enteros pares es igual que la cardinalidad del conjunto de números enteros.
Prueba: La suma de dos números enteros pares es par
| Considere dos números enteros pares arbitrarios x y y. | Aserción inicial |
| Un número entero par se puede escribir como 2a donde está un número entero a. | Definición un número entero par. |
| Demostraremos que existe un número entero c tales que x + y = 2c. | Demanda |
| x y y se puede reescribir como x = 2a y y = 2b donde están números enteros a y b. | Aplique la definición de un número entero par. |
| La suma x + y se puede escribir como 2a + 2b. | 2a substituto para x y 2b para el y. |
| 2a + 2b se pueden escribir como 2(a + b). | Aplique la propiedad distributiva de la multiplicación. |
| Existe un número entero c = a + b. | Aplique la propiedad de encierro de números enteros y de la suma. |
| 2(a + b) se pueden entonces reescribir como 2(c) = 2c. | Substituya c para a + b. |
| QED. | La prueba es completa. |
Prueba: El producto de dos números enteros pares es par.
| Considere dos números enteros pares arbitrarios x y y. | Aserción inicial |
| Un número entero par se puede escribir como 2a donde está un número entero a. | Definición de un número entero par. |
| Demostraremos que existe un número entero c tales que x · y = 2c. | Demanda |
| x y y se puede reescribir como x = 2a y y = 2b donde están números enteros a y b. | Aplique la definición de un número entero par. |
| El producto x · y se puede escribir como 2a · 2b. | 2a substituto para x y 2b para el y. |
| 2a · 2b se puede escribir como 2 · (a · 2 · b). | Aplique la propiedad asociativa de la multiplicación. |
| Existe un número entero c = a · 2 · b. | Aplique la propiedad de encierro de números enteros y de la multiplicación. |
| 2 (a · 2 · b) se puede entonces reescribir como 2 (c) = 2c. | C substituta para a · b. |
| QED. | La prueba es completa. |
Citar este artÃculo como:
Número par. 2009-05-12. Enciclopedia de Todas las Palabras de la Matemáticas. Life is a Story Problem.org. http://www.allmathwords.org/es/e/evennumber.html.
Traducciones
créditos de imagen
- Todas las imágenes y manipulatives están por David McAdams a menos que estén indicadas de otra manera. Todas las imágenes de David McAdams son & de los derechos reservados; © Life is a Story Problem.org y se puede reproducir para el uso educativo no comercial solamente.
La historia de revisión
2009-05-12: Corrigió varios errores tipográficos (McAdams, David.)
2009-04-03: Traducido automáticamente por BabelFish (babelfish.yahoo.com.)
2009-01-04: Ecuación cambiada a la imagen (McAdams, David.)
2008-07-08: Versión inicial (McAdams, David.)
- Navegación
- Home
- Contenido
-
# A B C D E F G H I J L M N O P Q R S T U V X Y - Ayudas del profesor
- Demostraciones de la Clase
- Referencia recÃproca
- GeometrÃa de NYSDE
- LIASP
- LIASP Home
- Condiciones del uso
- PolÃtica de aislamiento
- Done a LIASP
- Estructura de la ayuda este sitio
- Sobre LIASP
- LIASP del Contacto
Enciclopedia de Todas las Palabras de la Matemáticas es un servicio de
Life is a Story Problem.org.
Los derechos reservados ©2005-2009 de Life is a Story Problem.org. Todos los derechos reservados.
 Este trabajo
se autoriza debajo de una
Creative Commons Attribution-Noncommercial-Share Alike 3.0 License
Este trabajo
se autoriza debajo de una
Creative Commons Attribution-Noncommercial-Share Alike 3.0 License