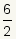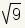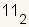Número: Una representación numérica de una cantidad.

Número

Un número es una representación de una cantidad. Una cantidad contesta a las preguntas, “cuántos?� y “cuánto?�

3 manzanas
Figura 1: 3 manzanas
 En el cuadro 1 hay tres manzanas. Podemos utilizar diversos caracteres para representar la cantidad:
3
tres
3.0
6/2
4-1
raíz cuadrada de 9
11 en la base 2
Cuadro 1: Representaciones de la cantidad 3
¿En cuántas maneras puede usted pensar para representar 3?

Palabras relacionadas

Numérico
Numérico
Numéricamente
Cantidad

Dígitos y valor de lugar

Los dígitos del número 374 son 3 en los ciento lugares, 7 en el lugar de los diez y 4 en los lugar.
Cuadro 2: Dígitos y valor de lugar

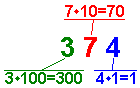
Cada dígito de un número tiene un valor. La posición del dígito en el número representa el valor de posición. Para los números decimales, los valores de posición son múltiplos de 10. El cuadro 2 demuestra un número sin una coma fraccionaria. Esto significa que el dígito en la extrema derecha en el número tiene un valor de posición de 1. El valor total del dígito es 4 · 1 = 4.

El dígito siguiente a la izquierda es '7'. El valor de posición de este dígito es 1 · 10 = 10. El valor total del dígito es 10 · 7 = 70. El dígito siguiente a la izquierda tiene un valor de posición de 10 · 10 = 100. El valor total del dígito es 3 · 100 = 300. El valor del número en el cuadro 2 está tan 300 + 70 + 4.

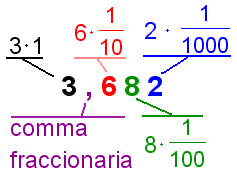
Los dígitos del número 3.682, 6 están en el décimo lugar, 8 está en el centésimo lugar, y 2 está en el milésimo lugar
Cuadro 3: Dígitos y valor de lugar a la derecha de la coma.

En el cuadro 3, el número 3.682 tiene una coma fraccionaria. El dígito a la izquierda de la coma como valor de posición de 1. El dígito a la derecha de la coma tiene un valor de posición de 1/10. Cada dígito a la derecha de la coma fraccionaria tiene más lejos un valor de posición de 1/10 del dígito anterior. Tan 6 tiene un valor total de 6 · 1/10 = 6/10. Los dos dígitos siguientes tienen valores de 8 · 1/100 = 8/100 y 2 · 1/1000. El valor del número entero es 3 + 6/10 + 8/100 + 2/1000.

Partes de un número

Partes de un número decimal: muestra, parte entera, decimal, parte menos de una
Cuadro 4: Partes de un número.
Un número puede consistir en dígitos, una separador milliares, una muestra positiva o negativa (+ o -), y un coma fraccionaire.

Otras representaciones de la cantidad

Siete marcas índice. Cada uno tiene marca es una recta segmento vertical.
Cuadro 5: Siete marcas índice
 Las cantidades se han representado en gran medida. Una forma que estaba en uso temprano era marcas índice. Cada recta cuenta como una. En el ejemplo en el cuadro 5, hay siete rectas. La cantidad representada es tan siete.

Hueso hecho muescas en de Turquía
Cuadro 6: Un hueso hecho muescas en, que se pudo haber utilizado como un instrumento musical o dispositivo de cuenta, fue encontrado en un sepulcro temprano de la edad de bronce (2900 A.C.) en Kenan Tepe, Turquía.
Fotógrafo: Bradley J. Parker
Los palillos y los huesos se han encontrado en los sitios arqueológicos con las muescas cortadas adentro les para hacer marcas índice. Las marcas índice tienen varios problemas. Cero no se puede representar por las marcas índice. También, los números muy grandes son torpes representar con tienen marcas. Solamente los números enteros positivos se pueden representar por las marcas índice.

Utilizaron los contadores y a los tableros de cobre amarillo de la cuenta para calcular números antes de que las calculadoras fueran inventadas. El cuadro 7 demuestra los contadores de cobre amarillo usados en Jamestown.
Marcadores contrarios de cobre amarillo excavados de Jamestown
Cuadro 7: Contadores de cobre amarillo excavados de Jamestown
De nuevos descubrimientos en Jamestown - sitio del primer establecimiento inglés acertado en América
Por la chaveta y J. Paul Hudson de Juan L.

Los números se han desarrollado como la mejor manera de representar cantidades. Pueden representar números positivos, cero, y números negativos. Pueden representar números muy grandes y muy pequeños. Pueden también representar cantidades no-enteras tales como 1.5. Los únicos números de la cosa no pueden representar exactamente son cantidades irracionales. Los dígitos en valores irracionales se encienden por siempre sin la repetición, así que un valor irracional no se puede representar con un número finito de dígitos. Otras representaciones tales como π y √2 se utilizan para representar números irracionales exactamente.

Tipos de números

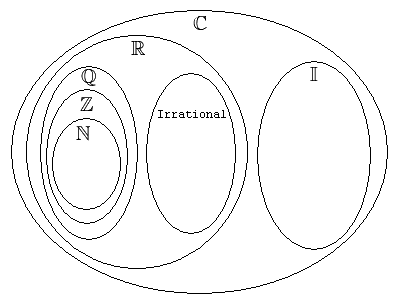
Diagrama de Venn de los tipos del número.
C: Número complejo
R: Número verdadero
El doble pegó I: Número imaginario
Q: Número racional
Z: Número entero (números enteros)
N: Número natural (que cuenta números)
Cuadro 8: Tipos del número

Los matemáticos han dividido números en grupos según sus propiedads. El cuadro 8 es un diagrama de Venn de los tipos del número. El grupo de números complejos contiene el resto de los grupos de números. Todos los números son números complejos. El cuadro 2 da las propiedads de los tipos de números.

Tipos de números
TipoSímboloDescripciónEjemplos
Número complejo ℂ Un número complejo es un número con una parte real y una partición imaginaria. La parte real es cualquier número real. La parte imaginaria es un número real multiplicado por i. i representa √-1. Puesto que el coeficiente de la parte imaginaria puede ser 0, todos los números reales son también números complejos.

Más información

  • McAdams, David. Número complejo. Toda la matemáticas redacta la enciclopedia. http://www.allmathwords.org/c/complexnumber.html.
  • Número complejo. Enciclopedia de Wikipedia. http://en.wikipedia.org/wiki/Complex_number
3+2i
-2.7+4i
e3.7i
Número verdadero ℝ Un número real es un número que se puede encontrar en la Recta numérica verdadero. Todos los números reales son también números complejos. Indicado matemáticamente: ℝ ⊂ ℂ.

Más información

  • McAdams, David. Número verdadero. Toda la matemáticas redacta la enciclopedia. http://en.wikipedia.org/wiki/Real_number.
  • Número verdadero. Enciclopedia de Wikipedia. http://en.wikipedia.org/wiki/Real_number.
4
3.74
e2.0
√5
π
3.5193
Número imaginario 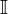El doble pegó I Un número imaginario es un número complejo sin la partición verdadera. Todos los números imaginarios son también números complejos.

Más información

 4i
3.74i
e3πi/2
√-3
Número racional ℚ Un número racional es un número real que se puede expresar como el razón de dos números enteros. Un número con un decimal de repetición es un número racional, como todos los decimales de repetición se pueden expresar como razón de números enteros. Todos los números racionales son también números reales. Indicado matemáticamente: ℚ ⊂ ℝ.

Más información

  • McAdams, David. Número racional. Toda la matemáticas redacta la enciclopedia. http://www.allmathwords.org/rationalnumber.html.
  • Número racional. Enciclopedia de Wikipedia. http://en.wikipedia.org/wiki/Rational_number.
4 ¿Por qué?
3/7
√9 ¿Por qué?
3.5193 ¿Por qué?
Número irracional Ninguno Un número irracional es un número que no se puede expresar como el razón de dos números enteros. El conjunto de números racionales combinó con el conjunto de números irracionales compone el conjunto de números reales.

Más información

  • McAdams, David. Número irracional. Toda la matemáticas redacta la enciclopedia. http://www.allmathwords.org/i/irrational.html.
  • Número irracional. Enciclopedia de Wikipedia. http://en.wikipedia.org/wiki/Irrational_number.
π
e
√5
Número entero ℤ Un número entero es un número entero o un cero positivo o negativo. Todos los números enteros son también números racionales. Esto es porque cualquier número entero se puede escribir a/1. Un número entero es la misma cosa que un número entero.

Más información

  • McAdams, David. Número entero. Toda la matemáticas redacta la enciclopedia. http://www.allmathwords.org/integer.html.
  • Número entero. Enciclopedia de Wikipedia. http://en.wikipedia.org/wiki/Integer.
4
7
√9 ¿Por qué?
3.0 ¿Por qué?
Número natural ℕ Un número natural es el conjunto de números enteros positivos: {1, 2, 3,…}. Éstos también se llaman cuenta de números. Todos los números naturales son también números enteros.

Más información

  • Número natural. Enciclopedia de Wikipedia. http://en.wikipedia.org/wiki/Natural_number.
4
6/2
Cuadro 2: Tipos de números

Más información

  • McAdams, David. Número complejo. AllMathWords.org. Life is a Story Problem.org. 2009-04-03. http://www.allmathwords.org/article.aspx?lang=en&id=Complex%20Number.
  • McAdams, David. Número entero. AllMathWords.org. Life is a Story Problem.org. 2009-04-03. http://www.allmathwords.org/article.aspx?lang=en&id=Integer.
  • McAdams, David. Número primero. AllMathWords.org. Life is a Story Problem.org. 2009-04-03. http://www.allmathwords.org/article.aspx?lang=en&id=Prime%20Number.
  • McAdams, David. Linea de Numero. AllMathWords.org. Life is a Story Problem.org. 2009-04-03. http://www.allmathwords.org/article.aspx?lang=en&id=Real%20Number.
  • McAdams, David. Número real. AllMathWords.org. Life is a Story Problem.org. 2009-04-03. http://www.allmathwords.org/article.aspx?lang=en&id=Number%20Line.
  • Wilson, Robin. 4000 años de números. Gresham College. 2009-04-03. Traducido automáticamente por babelfish.yahoo.com. http://www.gresham.ac.uk/event.asp?PageId=45&EventId=622.

Citar este artículo como:
Número. 2009-04-03. Enciclopedia de Todas las Palabras de la Matemáticas. Life is a Story Problem.org. http://www.allmathwords.org/es/n/number.html.

Traducciones

créditos de imagen

  • Todas las imágenes y manipulatives están por David McAdams a menos que estén indicadas de otra manera. Todas las imágenes de David McAdams son & de los derechos reservados; © Life is a Story Problem.org y se puede reproducir para el uso educativo no comercial solamente.

La historia de revisión


2009-04-03: Traducido automáticamente por BabelFish. (babelfish.yahoo.com.)
2008-12-02: Ecuaciones cambiadas a las imágenes (McAdams, David.)
2008-08-26: En el primer párrafo, representaciones organizadas de 3 en una tabla (McAdams, David.)
2008-06-08: Tipos agregados de números (McAdams, David.)
2008-06-07: Deletreo corregido (McAdams, David.)
2008-05-02: Representación revisada de números irracionales (McAdams, David.)
2008-03-22: Cambió la otra información al estándar actual (McAdams, David.)
2007-11-20: Versión inicial (McAdams, David.)

Enciclopedia de Todas las Palabras de la Matemáticas es un servicio de Life is a Story Problem.org.
Los derechos reservados ©2005-2009 de Life is a Story Problem.org. Todos los derechos reservados.
Creative Commons License Este trabajo se autoriza debajo de una Creative Commons Attribution-Noncommercial-Share Alike 3.0 License