Cómo inscribir un circunferencia en un triángulo

Lo sentimos, pero la GeoGebra Applet no se pudo iniciar. Por favor, asegúrese de que Java 1.4.2 (o posterior) está instalado y activo en su navegador ( Haga clic aquí para instalar Java ahora )
El manipulante 1: Triángulo inscrito. Creado con GeoGebra.
Chasque encendido los puntos azules en el manipulante y arrástrelo para cambiar el manipulante.
PasoEjemploDescripción
1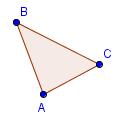Triángulo ABCComience con el Triángulo ABC.
2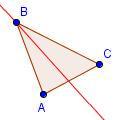Triángulo ABC con el bisectriz de un ángulo para el ABC del ángulo.Dibuje el bisectriz de ángulo ABC.
3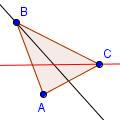Triángulo ABC con el bisectriz de un ángulo para el ángulo BCA.Dibuje el bisectriz de un ángulo del ángulo BCA. Para los pasos 2 y 3, cualquier dos ángulos pueden ser bisecados.
4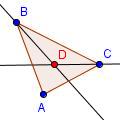Triángulo ABC con el punto D en la intersección de los dos bisectors del ángulo.Dibuje el punto D en la intersección de los bisectors del ángulo.
5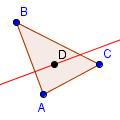Triángulo ABC con una recta a través del perpendicular del punto D a echar a un lado AB.Dibuje una recta a través de perpendicular del punto D para echar a un lado AB. Observe que esta recta puede ser perpendicular a los lados uces de los.
6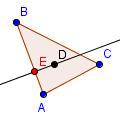Triángulo ABC con el punto E en la intersección de la recta perpendicular y del lado AB.Marque el punto E en la intersección del perpendicular y del AB lateral.
7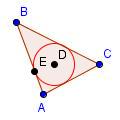Triángulo ABC con el circunferencia centrado en D con un radio de DE.Dibuje un circunferencia con el centro en D con un radio de DE.

Marca de cotejo Cheque de comprensión

Utilice el uso de GeoGebra abajo para construir el circunferencia el circunscribir sobre el rectángulo.

Lo sentimos, pero la GeoGebra Applet no se pudo iniciar. Por favor, asegúrese de que Java 1.4.2 (o posterior) está instalado y activo en su navegador ( Haga clic aquí para instalar Java ahora )
  1. Chasque encendido abajo la flecha de la construcción Botón de la construcción de GeoGebra. para abrir el menú de la construcción. Seleccione el artículo de menú Botón bisectriz del menú del ángulo de GeoGebra. bisectriz del ángulo. Entonces chasque encendido señala B, A, entonces C. Usted ha construido el bisectriz de un ángulo del CCB del ángulo.
  2. Ahora chasque encendido el punto A, B, entonces C. Usted ha construido el bisectriz de un ángulo del ABC del ángulo.
  3. Chasque encendido abajo la flecha del botón del menú del punto Botón del menú del punto de Geogebra.. Seleccione el botón del menú de los objetos Geogebra interseca el botón del menú de dos objetos de la intersección dos. Chasque encendido cada uno de los dos bisectors del ángulo. Señale D que aparezca en la intersección de los dos bisectors del ángulo sea el incentro.
  4. Chasque encendido la flecha en el botón bisectriz del menú del ángulo Botón bisectriz del menú del ángulo de GeoGebra. para abrir el menú de la construcción. Chasque encendido la recta perpendicular botón del menú Línea perpendicular botón de GeoGebra del menú.. Ahora chasque encendido el incentro (punto C) entonces un lado del triángulo. El punto donde la recta perpendicular interseca el lado del triángulo está en el circunferencia inscrita.
  5. Chasque encendido la intersección que dos objetos Geogebra interseca el botón del menú de dos objetos abotonan, después chascan encendido la recta perpendicular, y el lado a la cual él es perpendicular. El punto E aparece. El punto E está en el circunferencia inscrita.
  6. Chasque encendido el circunferencia con el centro a través de punto Círculo de GeoGebra con el centro a través de dos puntos del botón del menú.. Entonces chasque encendido el incentro (el punto D) entonces señala el E. El circunferencia que es exhausto es el circunferencia inscrita.

Para cambiar el manipulante, el primeros chascan encendido el botón Botón de la flecha de GeoGebra. del menú de la flecha. Entonces chasque encendido los puntos azules y arrástrelos para cambiar la figura.

Cuadro 2: Inscripción de un circunferencia en un triángulo.

Citar este artículo como:
Cómo inscribir un circunferencia en un triángulo. 2009-04-03. Enciclopedia de Todas las Palabras de la Matemáticas. Life is a Story Problem.org. http://www.allmathwords.org/es/h/htinscribetriangle.html.

Traducciones

créditos de imagen

  • Todas las imágenes y manipulatives están por David McAdams a menos que estén indicadas de otra manera. Todas las imágenes de David McAdams son & de los derechos reservados; © Life is a Story Problem.org y se puede reproducir para el uso educativo no comercial solamente.

La historia de revisión


2009-04-03: Traducido automáticamente por BabelFish. (babelfish.yahoo.com.)
2008-07-03: Versión inicial (McAdams, David.)

Enciclopedia de Todas las Palabras de la Matemáticas es un servicio de Life is a Story Problem.org.
Los derechos reservados ©2005-2009 de Life is a Story Problem.org. Todos los derechos reservados.
Creative Commons License Este trabajo se autoriza debajo de una Creative Commons Attribution-Noncommercial-Share Alike 3.0 License