Número irracional
Un número irracional es un número real que no se puede expresar como el razón de dos números enteros. Puesto que un número racional es un número real que se puede expresar como el razón de dos números enteros, éste significa que cualquier número real es racional o irracional, pero no puede ser ambos.
En matemáticas, una puede
representar
números de las maneras que enmascaran su identidad verdadera. Por ejemplo, la raÃz
cuadrada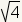 
del se puede
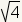reducir a 2, y tan no
a un número irracional, incluso si es representada usando una raÃz cuadrada.
Los ejemplos de números irracionales incluyen el π,
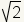, y
.
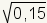Aquà están algunos ejemplos de los números que no son irracionales: 5,2,
, 3, y
.
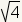Cheque de comprensión
Decida si cada número es irracional. Recuerde reducir y simplificar el número tanto cuanto sea posible. Entonces chasque “racional� o “irracional� para ver si usted tiene razón.
| Número | ¿Es irracional? |
|---|---|
|
Racional Irracional Correcto.Incorrecto. es irracional. No puede ser reducido más lejos, asà que no puede ser expresado como el razón de dos números enteros.
|
|
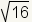
Racional Irracional Correcto.Incorrecto. 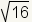es racional. Puede ser reducido a 4. 4 puede ser escrito 4/1, asà que es un número racional.
|
|
Racional Irracional Correcto.Incorrecto. es racional. Puede ser reducido a 2 que es un número racional.
|
| Cuadro 1: Racional o irracional | |
Citar este artÃculo como:
Número irracional. 2009-04-03. Enciclopedia de Todas las Palabras de la Matemáticas. Life is a Story Problem.org. http://www.allmathwords.org/es/i/irrational.html.
Traducciones
créditos de imagen
- Todas las imágenes y manipulatives están por David McAdams a menos que estén indicadas de otra manera. Todas las imágenes de David McAdams son & de los derechos reservados; © Life is a Story Problem.org y se puede reproducir para el uso educativo no comercial solamente.
La historia de revisión
2009-04-03: Traducido automáticamente por BabelFish. (babelfish.yahoo.com.)
2008-08-13: Cambió algunas construcciones de la matemáticas a las imágenes. Cheque agregado de la comprensión (McAdams, David.)
2007-07-12: Versión inicial (McAdams, David.)
- Navegación
- Home
- Contenido
-
# A B C D E F G H I J L M N O P Q R S T U V X Y - Ayudas del profesor
- Demostraciones de la Clase
- Referencia recÃproca
- GeometrÃa de NYSDE
- LIASP
- LIASP Home
- Condiciones del uso
- PolÃtica de aislamiento
- Done a LIASP
- Estructura de la ayuda este sitio
- Sobre LIASP
- LIASP del Contacto
Enciclopedia de Todas las Palabras de la Matemáticas es un servicio de
Life is a Story Problem.org.
Los derechos reservados ©2005-2009 de Life is a Story Problem.org. Todos los derechos reservados.
Este trabajo
se autoriza debajo de una
Creative Commons Attribution-Noncommercial-Share Alike 3.0 License