Rango
|
La rango de una función es todos los valores que la variable dependiente de la función puede tomar. Esto también significa que el rango de una función es todos los valores de la salida de la función. En la función |
Más información
- rango. buscon.rae.es. Real Academia Española. 2009-04-03. http://buscon.rae.es/draeI/SrvltConsulta?TIPO_BUS=3&LEMA=rango.
Citar este artículo como:
Rango. 2009-04-03. Enciclopedia de Todas las Palabras de la Matemáticas. Life is a Story Problem.org. http://www.allmathwords.org/es/r/range.html.
Traducciones
créditos de imagen
- Todas las imágenes y manipulatives están por David McAdams a menos que estén indicadas de otra manera. Todas las imágenes de David McAdams son & de los derechos reservados; © Life is a Story Problem.org y se puede reproducir para el uso educativo no comercial solamente.
La historia de revisión
2009-04-03: Traducido automáticamente por BabelFish. (babelfish.yahoo.com.)
2008-12-31: Ecuaciones cambiadas del HTML a las imágenes. Gama corregida del ejemplo de y>0 a y>=0 (McAdams, David.)
2008-12-23: Cuadro agregado 1 (McAdams, David.)
2008-09-04: Agregado '' más información '' (McAdams, David.)
2008-04-22: Referencia agregada a la gama de una función (McAdams, David.)
2008-02-27: Acoplamientos calientes convertidos del vocabulario del Javascript al HTML (McAdams, David.)
2007-07-12: Versión inicial (McAdams, David.)
- Navegación
- Home
- Contenido
-
# A B C D E F G H I J L M N O P Q R S T U V X Y - Ayudas del profesor
- Demostraciones de la Clase
- Referencia recíproca
- Geometría de NYSDE
- LIASP
- LIASP Home
- Condiciones del uso
- Política de aislamiento
- Done a LIASP
- Estructura de la ayuda este sitio
- Sobre LIASP
- LIASP del Contacto
Enciclopedia de Todas las Palabras de la Matemáticas es un servicio de
Life is a Story Problem.org.
Los derechos reservados ©2005-2009 de Life is a Story Problem.org. Todos los derechos reservados.
 Este trabajo
se autoriza debajo de una
Creative Commons Attribution-Noncommercial-Share Alike 3.0 License
Este trabajo
se autoriza debajo de una
Creative Commons Attribution-Noncommercial-Share Alike 3.0 License
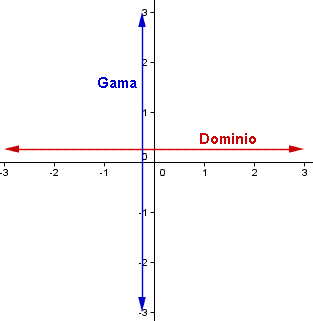
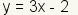 ,
el rango está sin restricción, significando que puede adquirir cualquier valor.
Sin embargo, para los
,
el rango está sin restricción, significando que puede adquirir cualquier valor.
Sin embargo, para los
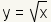 ,
la rango está
,
la rango está  ,
puesto que la función de raíz cuadrada vuelve solamente números no negativos.
,
puesto que la función de raíz cuadrada vuelve solamente números no negativos.