Enciclopedia de Todas las Palabras de la Matemáticas Home Page -

Solucionar una ecuación

La mayoría de los problemas de matemáticas que usted encontrará en álgebra implican el solucionar de ecuaciones. La idea es encontrar una solución a la ecuación. Una solución es un conjunto de uno o más valores que, cuando están substituidos para las variables, hagan la ecuación verdad.

Solucionar ecuaciones es una de las habilidades más importantes de la matemáticas a aprender. Hay varias clases de ecuaciones que usted encontrará en sus estudios:

Escoja las ecuaciones variables del grado uno por ejemplo x+3 = 2x-4. La meta en solucionar estas ecuaciones es conseguir la variable por sí mismo en un lado del signo igual. Qué se deja en el otro lado de la ecuación es el valor de la variable.
Escoja las ecuaciones variables del grado dos por ejemplo 2x²-3x+4 = 0. La fórmula cuadrático se utiliza para estas ecuaciones cuadráticos.
Dos ecuaciones variables del grado uno por ejemplo y = x-4. Estas ecuaciones son ecuaciones lineares. Pueden ser representadas gráficamente como recta. Las ecuaciones lineares con dos variables tienen soluciones infinitas.
Dos ecuaciones de dos variables, cada uno que es grado uno por ejemplo y = 3x + 7, y=-x-4. Esto se llama un sistema linear. Los sistemas lineares no tienen ninguna solución, una solución, o soluciones infinitas.

Hay otros tipos de ecuaciones para solucionarle puede encontrar en clases más avanzadas. No serán discutidas aquí.

�?ndice del artículo

Qué significa solucionar una ecuación?
Propiedad de los números usados para solucionar ecuaciones
Usando la suma y la resta para solucionar una ecuación
Usando la multiplicación para solucionar una ecuación
Usando la división para solucionar una ecuación
Usando la propiedad distributiva para solucionar una ecuación
Solucionando una ecuación gráficamente
Solucionar una ecuación cuadrático
Solucionar una ecuación variable múltiple

¿Qué significa solucionar una ecuación?

Para solucionar una ecuación es descubrir lo que dice la ecuación a una sobre los valores posibles de una o más variables. Tome la ecuación x+3 = 2x-1. ¿Qué esta ecuación dice a una sobre el valor de x? Para descubrir, solucione la ecuación.

Solucionar una ecuación linear de una variable implica el conseguir de la variable en un lado del signo igual por sí mismo. Para hacer éste utiliza las propiedads de números.

Propiedad de los números usados para solucionar una ecuación

Propiedad	Ejemplo	Descripción
Propiedad desumar cero	Dado un número real `x`; `x+0 = x`	Cero suma a cualquier igual del número el número original.
Propiedad de la suma de la igualdad	Dado tres números reales `a`, `b`, y `c`; si `a=b` entonces `a+c = b+c`	Si dos números son iguales, después de agregar el mismo valor a cada número, la suma siga siendo igual.
Propiedad de la resta de la igualdad	Dado tres números reales `a`, `b`, y `c`; si `a=b` entonces `ac = bc`	Si dos números son iguales, después de restar el mismo valor de cada número, la diferencia siga siendo igual.
Propiedad de multiplicarse por 1	Dado números reales `x`; `1·x = x`	Cualquier número se multiplicó por `1` se iguala.
Propiedad distributiva de la multiplicación sobre la suma y la resta	Dé 3 números reales `a`, `b`, y `c`; `a(b+c) = ab+ac`	Un número multiplicado por una suma es igual a la suma del número multiplicado por cada término.
Propiedad transitiva de la igualdad	Dado tres números reales `a`, `b`, y `c`; si `a=b` y `b=c` entonces `a=b`	Si dos números son iguales al mismo otro número, son iguales el uno al otro.
Cuadro 1: Propiedad de los números usados para solucionar una ecuación

Usando la suma y la resta para solucionar una ecuación

Comience con la ecuación x+3 = 5. Puesto que la meta es conseguir x por sí mismo, uno necesita hacer algo sobre los 3 que se agrega al x. Para deshacer la suma, utilice la resta:

Paso	Ecuación	Descripción
1	x+3 = 5	Ecuación original
2	(x+3) - 3 = 5-3	Propiedad de la resta de la igualdad.
3	(x+3)+ (- 3) = 5-3	Definición de la resta.
4	x+ (3+ (- 3)) = 5-3	Propiedad asociativa de la suma.
5	x+0 = 2	Simplifique ambos lados de la ecuación.
6	x = 2	Propiedad de la suma por cero.
7	(2)+3 = 5 5 = 5	Compruebe el trabajo substituyendo la solución nuevamente dentro de la ecuación.
Cuadro 2: Solucionando `x+3 = 5.`

Ahora comience con la ecuación x-2 = 1. Puesto que la suma deshace la resta, utilice la propiedad de la suma de la igualdad.

Paso	Ecuación	Descripción
1	x-2 = 1	Ecuación original
2	(x-2)+2 = 1+2	Propiedad de la suma de la igualdad.
3	(x+(-2))+2 = 1+2	Definición de la resta.
4	x+((-2) +2) = 1+2	Propiedad asociativa de la suma.
5	x+0 = 3	Simplifique ambos lados de la ecuación.
6	x = 3	Propiedad de la suma por cero.
7	(3) - 2 = 1 1 = 1	Compruebe el trabajo substituyendo la solución nuevamente dentro de la ecuación.
Cuadro 3: Solucionando `x-2 = 1.`

Usando la multiplicación para solucionar una ecuación

Comience con la ecuación x÷3 = 6. Una vez más uno quiere conseguir el x por sí mismo en un lado de la ecuación. Para deshacer la multiplicación, utilice la división:

Paso	Ecuación	Descripción
1	x÷3 = 6	Ecuación original
2	(x÷3)·3 = 6·3	Propiedad de la multiplicación de la igualdad.
3	x·(3÷3) = 6·3	Propiedad asociativa de la multiplicación.
4	x·1 = 18	Simplifique ambos lados de la ecuación.
5	x = 18	Propiedad de la multiplicación por 1.
6	18÷3 = 6 6 = 6	Compruebe el trabajo substituyendo la solución nuevamente dentro de la ecuación.
Cuadro 4: Solucionando `x÷3 = 6.`

Usando la división para solucionar una ecuación

Al usar la división para solucionar una ecuación, una debe estar segura de no dividir por cero. Puesto que la división por cero es indefinida, la división por cero dará resultados indeseables e incorrectos. Comience con la ecuación 3x = 6.

Paso	Ecuación	Descripción
1	3x = 6	Ecuación original
2	(3x) ÷3 = 6÷3	Propiedad de la división de la igualdad.
3	(x·3)÷3 = 6÷3	Propiedad comutativa de la multiplicación.
4	x·(3÷3) = 6÷3	Propiedad asociativa de la multiplicación.
5	x·1 = 2	Simplifique ambos lados de la ecuación.
6	x = 2	Propiedad de la multiplicación por 1.
7	3·2 = 6 6 = 6	Compruebe el trabajo substituyendo la solución nuevamente dentro de la ecuación.
Cuadro 5: Solucionando `3x = 6.`

Usando la propiedad distributiva para solucionar una ecuación

La propiedad distributiva de la multiplicación sobre la suma y la resta se utiliza a menudo para solucionar una ecuación. El ejemplo en el cuadro 6 utiliza la propiedad distributiva para quitar paréntesis.

Paso	Ecuación	Descripción
1	3 (x-4) = 3	Ecuación original
2	3·x-3·4 = 3	Propiedad distributiva de la multiplicación sobre la suma y la resta.
3	3x-12 = 3	Simplifique.
4	(3x-12) +12 = 3+12	Propiedad de la suma de la igualdad.
5	(3x+^-12) +12 = 3+12	Definición de la resta.
6	3x+ (^-12+12) = 3+12	Propiedad asociativa de la suma.
7	3x+0 = 15	Simplifique.
8	3x = 15	Propiedad de la suma por cero.
9	x·3 = 15	Propiedad comutativa de la multiplicación
10	x·3÷3 = 15÷3	Propiedad de la división de la igualdad.
11	x·1 = 5	Simplifique ambos lados de la ecuación.
12	x = 5	Propiedad de la multiplicación por 1.
13	3 (5-4) = 3 3·1 = 3 3 = 3	Compruebe el trabajo substituyendo la solución nuevamente dentro de la ecuación original.
Cuadro 6: Solucionar `3(x-4) = 3.`

El ejemplo en el cuadro 7 utiliza la propiedad distributiva para combinar dos términos que contienen la misma variable.

Paso	Ecuación	Descripción
1	3x = 2x + 3	Ecuación original
2	3x - 2x = 2x - 2x + 3	Propiedad de la suma de la igualdad.
3	3x - 2x = 0 + 3	Simplifique.
4	3x - 2x = 3	Propiedad de la suma por cero.
5	x(3 - 2) = 3	Propiedad distributiva de la multiplicación sobre la suma y la resta.
6	x·1 = 3	Simplifique.
7	x = 3	Propiedad de multiplicarse por 1.
8	3·3 = 2·3 + 3 9 = 6 + 3 9 = 9	Compruebe el trabajo substituyendo la solución nuevamente dentro de la ecuación.
Cuadro 7: Solucionando `3x = 2x + 3`.

Solucionando una ecuación gráficamente

Esta sección describe cómo utilizar una calculadora de representación gráfico gráficamente TI-83 o TI-84 para encontrar la raíz media de x3-0.5x2-2x+1. La mayoría de las calculadoras de representación gráfico gráficamente tienen una manera de solucionar ecuaciones gráficamente. Compruebe el manual del usuario para saber si hay su calculadora.

Paso	Pantalla	Descripción
1		Chasque el botón del <CLEAR> hasta que usted tenga una pantalla en blanco.
2		Chasque el botón del <Y=> en la fila superior para ver la pantalla de representación gráfico gráficamente de la ecuación. Si hay algunas ecuaciones que demuestran, utilice la llave del <CLEAR> y hacia arriba y hacia abajo las flechas para borrar todas las ecuaciones. Entonces chasque la llave de flecha ascendente hasta que esté en la posición superior.
3		Incorpore la ecuación `x³-0.5x²-2x+1` usando los golpes de teclado siguientes: <X, T, ?, n>, <^>, <3>, <->, <0>, <.>, <5>, <X, T, ?, n>, <x2>, <->, <2>, <x>, <+>, <1>.
4		Chasque encendido el botón del <WINDOW> para cargar la pantalla de representación gráfico gráficamente del parámetro de la ventana. Utilice las llaves del número y hacia arriba y hacia abajo los botones de la flecha para incorporar los parámetros de la ventana como demostración en la imagen de pantalla. Al incorporar números negativos, cerciórese de utilizar < (-) > la llave en la fila inferior de la calculadora. Los medios etiquetados dominantes del <-> restan, para no negar.
5		Chasque el botón del <GRAPH> en la fila superior de la calculadora. El gráfico de `x³-0.5x²-2x+1` aparecerá en la ventana que usted especificó.
6		Chasque el botón del <ZOOM> para ver el menú del zumbido.
7		Chasque abajo el botón de la flecha una vez para seleccionar la opción 2-Zoom del menú adentro.
8		Chasque la llave del <ENTER> en la esquina correcta inferior de la calculadora para volver al gráfico con la opción del zumbido activada.
9		Chasque el botón de la flecha derecha hasta que los pelos cruzados estén cerca de la intercepción media. Los números en la parte inferior de la pantalla cambian para demostrarle los coordenadas del pelo cruzado.
10		Chasque el botón del <ENTER> para enfocar adentro en los coordenadas del zumbido.
11		Chasque encendido el botón de la flecha izquierda hasta que los pelos cruzados estén sobre la intercepción. Los coordenadas del zumbido deben ser x=.5 y y=0. La intercepción correcta es x=0.5. Usted puede chascar encendido la llave de entrada otra vez para cerciorarse de que usted está tan cerca a la intercepción como sea posible.
Cuadro 8: Usando la calculadora TI-83/84 para encontrar una raíz de `x³-0.5x²-2x+1`.

Solucionar una ecuación cuadrático

Las ecuaciones cuadráticos en la forma ax² + bx + c = 0 se solucionan usando la fórmula cuadrático: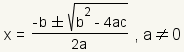

x= (- raíz de b+-square (b^2-4ac))¡/(2a) a!=0

La a, el b y la c en la fórmula cuadrático son la a, el b y la c en la ecuación cuadrático. Debido a el ± en la ecuación, una ecuación cuadrático puede tener dos soluciones.

Si el discriminante b² - 4ac es mayor de cero, la ecuación cuadrático tiene dos soluciones verdaderas. Una solución real es una solución que es un número real. Si el b² discriminante -4ac es 0, la ecuación cuadrático tiene una solución verdadera. Si el discriminante b² - ac es menos de cero, la ecuación cuadrático tiene dos soluciones complejas. Una solución compleja es una solución que es un número complejo.

El solucionar usando la ecuación cuadrático
Paso	Ecuación	Descripción
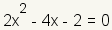		Ecuación a solucionar
1		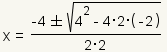Substituya `a = 2`, `b = -4` y `c = -2` en la fórmula cuadrático.
2		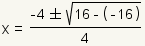Simplifican exponentes y la multiplicación dentro de paréntesis.
3		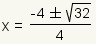Simplifican la resta dentro de paréntesis.
4		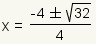Desde `32 = 16·2` y `√16·√2 = 4√2`, reescriben el radical como `4√2`.
5		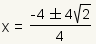Utilice la propiedad distributiva de la multiplicación sobre la suma y la resta para partir la fracción en dos fracciones.
6		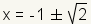Simplifique cada fracción.
7		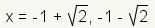Cambie el `±` en dos ecuaciones, una usando `+` y la otra usando `-`. Esta ecuación cuadrático tiene 2 soluciones.
Cuadro 9: Solucionando `2x² - 4x - 2 = 0` usando la fórmula cuadrático.

Solucionar una ecuación variable múltiple

Al solucionar una ecuación variable múltiple, una soluciona para una variable. Por ejemplo, dado la ecuación x + y = 2, una puede solucionar para el x variable o para el variable y. En este ejemplo solucionaremos para el y.

`x + y = 2`	Ecuación a solucionar en forma estándar
`x + y - x = 2 - x`	Reste x de ambos lados.
`y = 2 - x`	Simplifique el lado izquierdo de la ecuación.
`y = - x + 2`	Ponga la ecuación en forma de la pendiente y la intercepción.
Cuadro 10: El solucionar para y

Citar este artículo como:

Solucionar una ecuación. 2009-04-03. Enciclopedia de Todas las Palabras de la Matemáticas. Life is a Story Problem.org. http://www.allmathwords.org/es/s/solvingequation.html.

Traducciones

Click here to see this article in English.

créditos de imagen

Todas las imágenes y manipulatives están por David McAdams a menos que estén indicadas de otra manera. Todas las imágenes de David McAdams son & de los derechos reservados; © Life is a Story Problem.org y se puede reproducir para el uso educativo no comercial solamente.

La historia de revisión

2009-04-03: Traducido automáticamente por BabelFish. (babelfish.yahoo.com.)
2008-07-25: Versión inicial (McAdams, David.)

#	A	B	C	D
E	F	G	H	I
J	L	M	N	O
P	Q	R	S	T
U	V	X	Y

Enciclopedia de Todas las Palabras de la Matemáticas es un servicio de Life is a Story Problem.org.
Los derechos reservados ©2005-2009 de Life is a Story Problem.org. Todos los derechos reservados.
Este trabajo se autoriza debajo de una Creative Commons Attribution-Noncommercial-Share Alike 3.0 License