Reglas de la fracción

el numerador/el denominador se define como numerador dividido por denominador.
Cuadro 1: Fracción

Las reglas de la fracción son un sistema de las reglas algebraicas para trabajar con las fracciones. Una fracción tiene un numerador y un denominador. Una fracción representa una operación de la división. El numerador es el dividendo. El denominador es el divisor.

Reglas de la fracción
OperaciónEcuacionesEjemplosDescripción
Adición de dos fracciones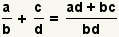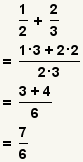(a/b)+ (c/d)= ()/(de ad+bc BD)(el 1/2) + (2/3)= (1*3+2*2)/(2*3)= (3+4)/6=7/6Para agregar fracciones, transforme cada fracción así que tienen un denominador común. Agregue los numeradores y utilice el denominador común como el denominador. Reduzca la fracción. Vea las operaciones en fracciones: Adición y resta.
Restar dos fracciones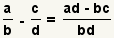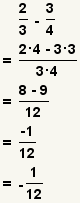(a/b) - (c/d)= ()/(del anuncio-a.C. BD)(2/3) - (3/4)= (2*4-3*3)/(3*4)= (8-9) /12= (- 1) /12=-1/12Para restar fracciones, transforme cada fracción así que tienen un denominador común. Reste los numeradores y utilice el denominador común como el denominador. Reduzca la fracción. Vea las operaciones en fracciones: Adición y resta.
Multiplicar dos fracciones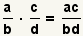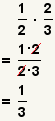(a/b)* (c/d)= ()/(de la CA BD)(5/12) *4= (5*4)/12= (5*4)/(3*4)=5/4Para multiplicar fracciones, multiplique los numeradores y multiplique los denominadores. Reduzca la fracción. Vea las operaciones en fracciones: Multiplicación.
Multiplicar una fracción y un número entero.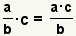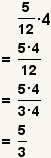(a/b)*C= (CA) /b(el 1/2) * (2/3)= (1*2)/(2*3)=1/3Para multiplicar una fracción y un número entero, multiplique el numerador por el número entero. Sigue habiendo el denominador sin cambiar. Reduzca la fracción si es posible.
División de dos fracciones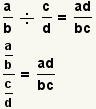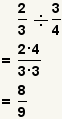(a/b)/(c/d)= ()/(del anuncio a.C.)(2/3)* (3/4)= (2/3)* (4/3)= (2*4)/(3*3)=8/9Para dividir fracciones, mueva de un tirón el divisor upside-down entonces se multiplican por el dividendo. Reduzca la fracción. Vea las operaciones en fracciones: División.
División de una fracción por un número entero.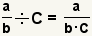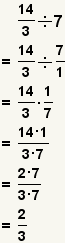(a/b)/C=a/(b*C)(14/3)/7= (14/3)/(7/1)= (14/3)* (1/7)= (14*1)/(3*7)= (2*7)/(3*7)=2/3Para dividir una fracción por un número entero, convierta el número entero a una fracción, la divisoria las fracciones.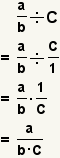
(a/b)/C= (a/b)/(C/1)= (a/b)* (1/C)=a/(b*C)
Aumento de una fracción a una energía.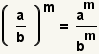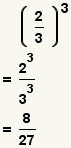(a/b)^m= (a^m)/(b^m)(2/3)^3= (2^3/3^3)=8/27Vea las operaciones en fracciones: Exponenciación.
Convertir un número mezclado a una fracción incorrecta.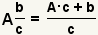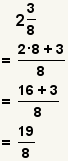2+ (3/8)= (2*8+3)/8= (16+3)/8=19/8Para convertir un número mezclado a una fracción incorrecta, multiplique la parte entera por el denominador y agregue el producto al numerador. Sigue habiendo el denominador sin cambiar. Vea cómo convertir un número mezclado a una fracción.
Convertir una fracción incorrecta a un número mezclado.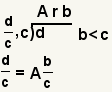21/5, 21=4*5+1, 21/5=4+ (1/5)2+ (3/8)= (2*8+3)/8= (16+3)/8=19/8Para convertir una fracción incorrecta a un número mezclado, divida el numerador por el denominador usando un resto. El número mezclado es el razón más el resto dividido por el denominador. Vea cómo convertir una fracción a un número mezclado.
Ponga a cero el numerador.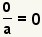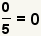¡0/a=0, a!=00/5=0Aplicando la propiedad de multiplicarse por cero, un numerador cero con un denominotor cero es cero. Vea la propiedad de multiplicarse por 0.
Ponga a cero el denominador.a/0=undefined8/0=undefinedPuesto que la división por cero es indefinida, un denominador cero hace la fracción indefinida.
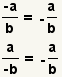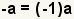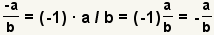Un signo de menos.(- a) /b=- (a/b), a (- b) = (a/b)(- 3) /2=- (3/2), 3 (- 2) = (3/2)Puesto que - *a del a= (- 1), aplique la propiedad asociativa de la multiplicación para conseguir (- a) /b= (- 1) *a/b= (- 1) *a/b=- (a/b)
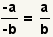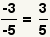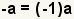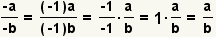Dos signos de menos.(-)/(de a - b) =a/b(- 3)/(- 5) =3/5Puesto que - *a del a= (- 1), aplique la propiedad asociativa de la multiplicación para conseguir (- a)/(- b) = ((- 1) *a)/((- *b)= de 1) (- 1)/(- 1) *a/b=1*a/b=a/b
Si una fracción tiene el mismo numerador y denominador diferentes a cero, el valor de la fracción es 1.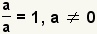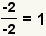¡a/a=1, a!=0(- 3)/(- 2) =1Cualquier cosa a menos que 0 dividido por sí mismo sea 1.
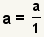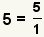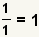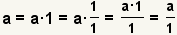Cualquier número entero se puede hacer en una fracción.a=a/15=5/1Puesto que 1/1=1, aplique la propiedad de multiplicarse por 1: a=a*1=a* (1/1)= (a*1)/1=a/1. Vea la propiedad de multiplicarse por 1.
Reducción de fracciones.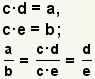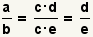c*d=a, c*e=b, a/b= (c*d)/(c*e)=d/e12/18= (6*2)/(6*3)=2/3Dado dos valores arbitrarios a y b, y los valores c, d, y e tales que a=c*d y b=c*e 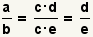a/b= (c*d)/(c*e)=d/e. Vea la reducción de fracciones.
Fracciones del edificio.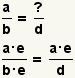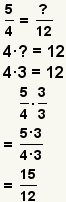\ arsenal {dado a/b, y d; hallazgo c tales que a/b=c/d. Existe e tales que b*e = D. Entonces (a/b)* (e/e)= (a*e)/(b*e) = c/d¿5/4=?/12. ¿4*?=12. 4*3=12. (5/4)* (3/3)= (5*3)/(4*3)=15/12Dado una fracción a/b y un número d que es un múltiplo de d, hallazgo e tales que b·e=d, entonces a/b= (a·e) (b·e).
Operaciones en fracciones complejas.Simplifique las fracciones complejas, después utilice las reglas para las fracciones simples.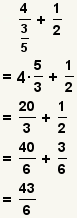4 (3/5)+1/2=4* (5/3)+1/2=20/3+1/2=40/6+3/6Para manipular una fracción compleja, conviértala a una fracción simple, después siga las reglas para las fracciones simples. Vea la fracción compleja.
Convertir un número devérticel a una fracción.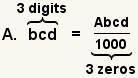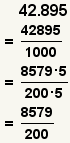A.bcd=Abcd/100042.895=42895/1000=8579/200Para convertir un devérticel a una fracción, cambie el devérticel a un número entero y divídalo por 10n donde está el número n de dígitos después de la coma.
Convertir un porcentaje a una fracción.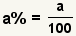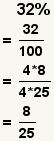a%=a/10032%=32/100= (8*4)/(25*4)=8/25Para convertir un porcentaje a una fracción, utilice el porcentaje como el numerador, 100 como el denominador, después simplifiqúelo.
Comparar fracciones con denominadores semejantes.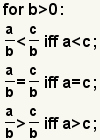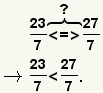(a/b)< (c/b), a<c de b>0 si y solamente si ; (a/b)= (c/b), a=c de b>0 si y solamente si ; (a/b)> (c/b), a>c de b>0 si y solamente si ¿23/7<=>?27/8-> (23/7)<27/7Para comparar fracciones con denominadores semejantes, compare los numeradores. La relación entre las fracciones es igual que la relación entre los denominadores.
Comparar fracciones con denominadores desemejantes.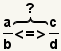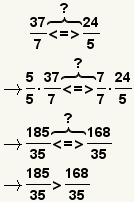¿(a/b)=?(c/d)¿37/7<=>?¿24/5-> (37/7)* (5/5)<=>?¿(24/5)* (7/7) - >185/35<=>?168/35->185/35>168/35Para comparar fracciones con denominadores desemejantes, para convertirlos a un devérticel o para transformarlos a un denominador común, entonces para compararlos.
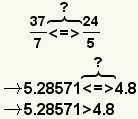¿37/7<=>?¿24/5->5.28571<=>?4.8->5.28571<4.8
Cuadro 1

Citar este artículo como:
Reglas de la fracción. 2009-04-03. Enciclopedia de Todas las Palabras de la Matemáticas. Life is a Story Problem.org. http://www.allmathwords.org/es/f/fractionrules.html.

Traducciones

créditos de imagen

  • Todas las imágenes y manipulatives están por David McAdams a menos que estén indicadas de otra manera. Todas las imágenes de David McAdams son & de los derechos reservados; © Life is a Story Problem.org y se puede reproducir para el uso educativo no comercial solamente.

La historia de revisión


2009-04-03: Traducido automáticamente por BabelFish. (babelfish.yahoo.com.)
2009-01-14: Versión inicial (McAdams, David.)

Enciclopedia de Todas las Palabras de la Matemáticas es un servicio de Life is a Story Problem.org.
Los derechos reservados ©2005-2009 de Life is a Story Problem.org. Todos los derechos reservados.
Creative Commons License Este trabajo se autoriza debajo de una Creative Commons Attribution-Noncommercial-Share Alike 3.0 License