Operaciones en fracciones
Una operación
es algo como la suma y la multiplicación. Una
operación en una fracción
aplica
una de estas operaciones a las fracciones.
Ã?ndice del artÃculo
Adición y resta de fracciones
Para agregar o restar fracciones, uno debe
primero encontrar un denominador común. Se utiliza el
menos denominador común
puesto que simplifica los cálculos.
Ejemplo 1 de la suma
| Paso | Expresiones | Descripción |
|---|
| 1 | 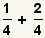 | Éstas son las fracciones a agregar. |
| 2 | 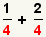 | Puesto que los denominadores son ya iguales, no hay necesidad de encontrar un menos denominador común. |
| 3 | 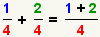 | Escriba una nueva fracción con la suma en superior y el denominador común en la parte inferior. |
| 4 | 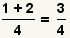 | Agregue el numerador. Puesto que el numerador 3 y el denominador 4 son relativamente primeros, la fracción no se puede simplificar más lejos. Se hace el problema. |
| Cuadro 1: Adición del ejemplo 1. de las fracciones. |
Ejemplo 2 de la suma
| Paso | Expresiones | Descripción |
|---|
| 1 | 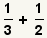 | Éstas son las fracciones a agregar. |
| 2 | 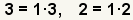 | El primer paso en encontrar el menos denominador común está encontrando la facturización primera de cada uno de los denominadores. |
| 3 | 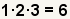 | Combine los factores primeros para conseguir el menos denominador común. 6 es el menos denominador común. |
| 4 | 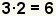 | Encuentre el número para multiplicarse por la primera fracción. ¿Puesto que el menos denominador común es 6, y el denominador de la primera fracción es 3, qué tiempos 3 igualan 6? |
| 5 | 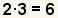 | Encuentre el número para multiplicarse por la segunda fracción. ¿Puesto que el menos denominador común es 6, y el denominador de la segunda fracción es 2, qué tiempos 2 igualan 6? |
| 6 |  | Utilizaremos la propiedad de multiplicarse por 1 para transformar las fracciones. |
| 7 | 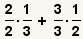 | Aplique la propiedad de multiplicarse por 1. |
| 8 | 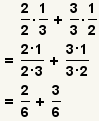 | Multiplique las fracciones. |
| 9 | 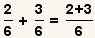 | Puesto que los denominadores son iguales, agregue los numeradores. |
| 10 | 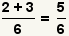 | Agregue el numerador. Puesto que el numerador 5 y el denominador 6 son relativamente primeros, la fracción no se puede simplificar más lejos. Se hace el problema. |
| Cuadro 2: Adición del ejemplo 2. de las fracciones. |
Ejemplo 3 de la suma
| Paso | Expresiones | Descripción |
|---|
| 1 | 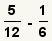 | Éstas son las fracciones a restar. |
| 2 | 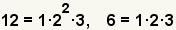 | El primer paso en encontrar el menos denominador común está encontrando la facturización primera de cada uno de los denominadores. |
| 3 | 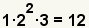 | Combine los factores primeros para conseguir el menos denominador común. 12 es el menos denominador común. |
| 4 | 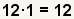 | Encuentre el número para multiplicarse por la primera fracción. ¿Puesto que el menos denominador común es 12, y el denominador de la primera fracción es 12, qué tiempos 12 igualan 12? 1 por 12 iguales 12. Esto significa que la primera fracción tiene ya el menos denominador común. |
| 5 | 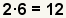 | Encuentre el número para multiplicarse por la segunda fracción. ¿Puesto que el menos denominador común es 12, y el denominador de la segunda fracción es 6, qué tiempos 6 igualan 12? |
| 6 | 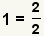 | Utilizaremos la propiedad de multiplicarse por 1 para transformar las fracciones. |
| 7 | 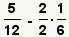 | Aplique la propiedad de multiplicarse por 1. |
| 8 | 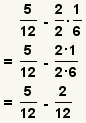 | Multiplique la fracción. |
| 9 | 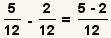 | Puesto que los denominadores son iguales, reste los numeradores. |
| 10 | 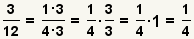 | El numerador y el denominador no son relativamente primeros. Encuentre y cancele el factor común. |
| Cuadro 3: Adición del ejemplo 3. de las fracciones. |
Caso general de la suma
Para derivar el caso general, comience con la suma de dos fracciones
arbitrarias:
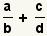
.
Los
denominadores
no son iguales, asà que las fracciones no pueden todavÃa ser agregadas. Puesto
que los denominadores son
b y
d,
b·d será
siempre un denominador común. Sin embargo,
b·d puede no ser el
menos denominador común.
Primero utilice la
propiedad de multiplicarse por 1. aplican la propiedad de multiplicarse por 1 a la fracción a conseguir
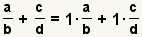
.
Pero, desde entonces
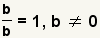
y

,
y
d/d substitutos en la expresión, consiguiendo
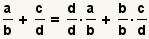
.
Multiplique las fracciones para conseguir
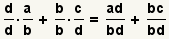
.
Puesto que los denominadores ahora son campo común, agregue los numeradores:
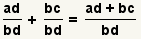
.
Podemos ahora concluir

.
Multiplicación de fracciones
Para multiplicar fracciones, multiplique los
numeradores de uno a y los denominadores de uno a:
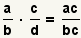
.
Ejemplo 1 de la multiplicación
| Paso | Expresiones | Descripción |
|---|
| 1 | 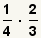 | Éstas son las fracciones a multiplicarse. |
| 2 | 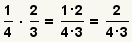 | Multiplique los numeradores y los denominadores. |
| 3 |  | AmplÃe el numerador y el denominador en factores. |
| 4 | 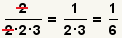 | Cancele los factores comunes, después multiplique hacia fuera el numerador y el denominador. Puesto que 1 es primero concerniente a 6, esta fracción no se puede reducir más lejos. Se hace el problema. |
| Cuadro 4: Multiplicación del ejemplo 1. de las fracciones. |
Ejemplo 2 de la multiplicación
| Paso | Expresiones | Descripción |
|---|
| 1 | 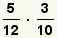 | Éstas son las fracciones a multiplicarse. |
| 2 | 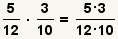 | Multiplique los numeradores y los denominadores. |
| 3 | 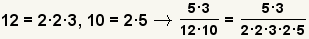 | AmplÃe el numerador y el denominador en factores. |
| 4 | 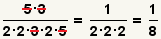 | Cancele los factores comunes, después multiplique hacia fuera el numerador y el denominador. Puesto que 1 es primero concerniente a 8, esta fracción no se puede reducir más lejos. Se hace el problema. |
| Cuadro 5: Multiplicación del ejemplo 2. de las fracciones. |
División de fracciones
Al dividir fracciones, utilice la propiedad de las fracciones que la división por una fracción es igual que multiplicándose por su recÃproco:
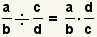
.
Ejemplo 1 de la división
| Paso | Expresiones | Descripción |
|---|
| 1 | 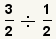 | Éstas son las fracciones a dividir. |
| 2 | 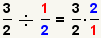 | Cambie el problema de la división en un problema de la multiplicación moviendo de un tirón el divisor. |
| 3 | 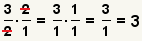 | Cancele los factores comunes y simplifique la fracción. |
| Cuadro 6: División del ejemplo 1. de las fracciones. |
Ejemplo 2 de la división
| Paso | Expresiones | Descripción |
|---|
| 1 | 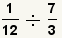 | Éstas son las fracciones a dividir. |
| 2 |  | Cambie el problema de la división en un problema de la multiplicación moviendo de un tirón el divisor. |
| 3 | 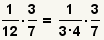 | Encuentre los factores comunes. |
| 4 | 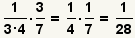 | Cancele los factores comunes y simplifique la fracción. |
| Cuadro 7: División del ejemplo 2. de las fracciones. |
Derivación de la regla de la división para las fracciones
| Paso | Expresiones | Descripción |
|---|
| 1 | 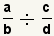 | Comience con una caja general de fracciones a dividir. a, b, c y d representan valores arbitrarios. |
| 2 | 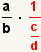 | La definición de la división es 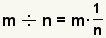 . Utilice la definición de la división para transformar el divisor. . Utilice la definición de la división para transformar el divisor. |
| 3 | 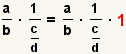 | Este paso utilizará la propiedad de multiplicarse por 1: 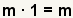 . Uso a la propiedad de multiplicarse por 1 a multiplicar el derecho por 1. . Uso a la propiedad de multiplicarse por 1 a multiplicar el derecho por 1. |
| 4 | 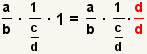 | Este paso utilizará la propiedad de dividir un valor por sà mismo:  . Utilice la propiedad de la substitución de la igualdad para substituir el 1 por . Utilice la propiedad de la substitución de la igualdad para substituir el 1 por 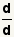 . . |
| 5 | 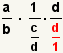 | Puesto que 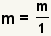 , substituya la d en el denominador de la fracción pasada por , substituya la d en el denominador de la fracción pasada por 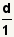 . . |
| 6 | 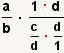 | Combine las dos fracciones a la derecha. |
| 7 | 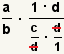 | Cancele las d. |
| 8 | 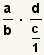 | Simplifique el denominador a la derecha. |
| 9 | 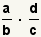 | Utilice el hecho con 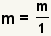 el cual el cual 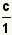 substituir substituir  . . |
| 10 | 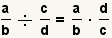 | Hemos demostrado eso 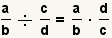 |
| Cuadro 8: Derivación de la regla de la división para las fracciones. |
Elevar de fracciones a una potencia
Si una fracción se elevar a una potencia, el numerador
y el denominador se pueden cada uno elevar a la misma potencia:
Exponenciación del ejemplo 1 de las fracciones
| Paso | Expresiones | Descripción |
|---|
| 1 | 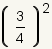 | Ésta es la fracción a elevar a una potencia. |
| 2 | 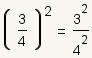 | Aplique la regla de la potencia para las fracciones. |
| 3 | 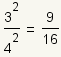 | Simplifique el numerador y el denominador. |
| Cuadro 6: Exponenciación del ejemplo 1. de las fracciones. |
Citar este artÃculo como:
Operaciones en fracciones. 2009-04-03. Enciclopedia de Todas las Palabras de la Matemáticas. Life is a Story Problem.org. http://www.allmathwords.org/es/o/operationsonfractions.html.
Traducciones
créditos de imagen
- Todas las imágenes y manipulatives están por David McAdams a menos que estén indicadas de otra manera. Todas las imágenes de David McAdams son & de los derechos reservados; © Life is a Story Problem.org y se puede reproducir para el uso educativo no comercial solamente.
La historia de revisión
2009-04-03: Traducido automáticamente por
BabelFish. (
babelfish.yahoo.com.)
2009-01-15: Versión inicial (
McAdams, David.)
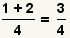
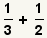
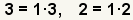
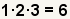
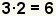
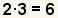

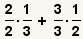
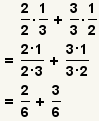
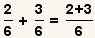
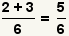
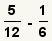
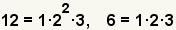
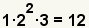
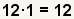
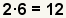
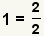
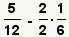
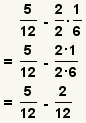
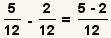
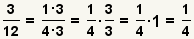
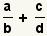 .
.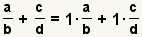 .
.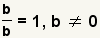 y
y  ,
,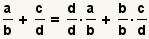 .
.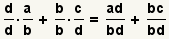 .
.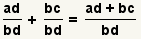 .
. .
.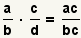 .
.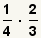
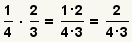

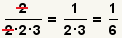
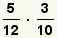
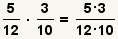
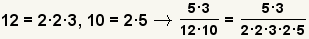
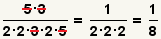
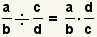 .
.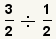

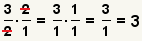
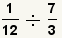

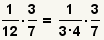
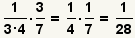
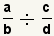
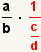
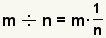 . Utilice la definición de la división para transformar el divisor.
. Utilice la definición de la división para transformar el divisor.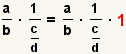
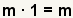 . Uso a la propiedad de multiplicarse por 1 a multiplicar el derecho por 1.
. Uso a la propiedad de multiplicarse por 1 a multiplicar el derecho por 1.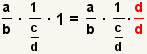
 . Utilice la propiedad de la substitución de la igualdad para substituir el 1 por
. Utilice la propiedad de la substitución de la igualdad para substituir el 1 por 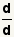 .
.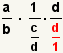
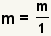 , substituya la d en el denominador de la fracción pasada por
, substituya la d en el denominador de la fracción pasada por 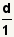 .
.

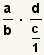
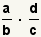
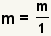 el cual
el cual 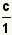 substituir
substituir  .
.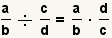
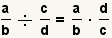
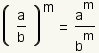
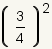
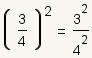
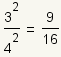
 Este trabajo
se autoriza debajo de una
Creative Commons Attribution-Noncommercial-Share Alike 3.0 License
Este trabajo
se autoriza debajo de una
Creative Commons Attribution-Noncommercial-Share Alike 3.0 License