Usando las matrices para solucionar sistemas lineares

Un sistema linear se puede solucionar usando matrices. Cada fila en la matriz representa una ecuación linear. Cada columna en la matriz representa una variable en las ecuaciones lineares.

Transformación de un sistema linear a una matriz

Comience con el sistema linear

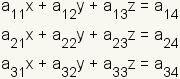
a11*x+a12*y+a13*z=a14; a21*x+a22*y+a23*z=a24; a31*x+a32*y+a33*z=a34

donde 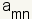amn está un coeficiente. Organice el sistema linear por la variable para las columnas y las ecuaciones para las filas:

esconda, x-coeficiente, y-coeficiente, z-coeficiente, valor;a11*x, +a12*y, +a13*z, =a14; a21*x, +a22*y, +a23*z, =a24; a31*x, +a32*y, +a33*z, =a34

Ahora caiga las variables y a los operadores y dibuje los soportes de la matriz alrededor de los valores:

matriz, fila 1: a11, a12, a13, a14; fila 2: a21, a22, a23, a24; fila 3: a31, a32, a33, a34

Ejemplo: Comience con el sistema linear

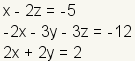x-2z=-5; -2x-3y-3z=-12; 2x+2y=2.
Ahora organícelo en filas y columnas.
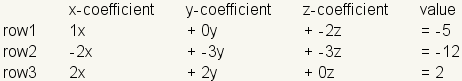esconda, x-coeficiente, y-coeficiente, z-coeficiente, valor; reme el 1:1 x, +0y, +-2z, - 5; reme el 2:-2 x, +-3y, +-3z, - 12; reme el 3:2 x, +2y, +0z, 2.
Ahora ponga el sistema en la notación de matriz.
1:1,0 de la fila de la matriz, - 2, - 5; reme el 2:-2, - 3, - 3, - 12; reme el 3:2,2,0,2.

Reme las operaciones

Hay las operaciones de la fila que se pueden hacer en una matriz que, si está hecha correctamente, ayude a transformar la matriz en una solución al sistema linear representado por la matriz. Estas operaciones son:

  • Multiplicación escalar de una fila: Cualquier fila se puede multiplicar por cualquier número real diferente a cero.
  • Sumar de la fila: Cualquier fila se puede sumar a cualquier otra fila y la suma se utilice para substituir cualquier fila.
  • Filas comerciales: Cualquier dos filas pueden ser intercambiadas.

Multiplicación escalar de una fila

La multiplicación escalar de una fila es como la multiplicación escalar de la matriz entera, pero se hace a solamente una fila. En el ejemplo siguiente, la fila 1 es multiplicada por 2.

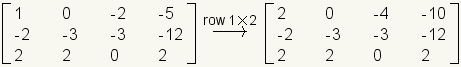1:1,0 de la fila de la matriz, - 2, - 5; reme el 2:-2, - 3, - 3, - 12; reme el 3:2,2,0,2; flecha que indica la fila 1 por 2; 1:2,0 de la fila de la matriz, - 4, - 10; reme el 2:-2, - 3, - 3, - 12; reme el 3:2,2,0,2.
Al multiplicar filas, es generalmente el mejor utilizar números enteros siempre que sea posible. Esto hace pasos posteriores en solucionar el sistema linear mucho más fáciles.

Suma de filas

Al sumar filas, los elementos correspondientes de cada fila se agregan juntos. Los resultados se ponen en cualquiera de las filas que son agregadas. En el ejemplo siguiente, la fila 1 se agrega para remar 2 y el resultado puesto en la fila 2.

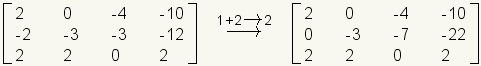1:2,0 de la fila de la matriz, - 4, - 10; reme el 2:-2, - 3, - 3, - 12; reme el 3:2,2,0,2; la flecha que indica la fila 1 más 2 entra la fila 2; 1:2,0 de la fila de la matriz, - 4, - 10; reme el 2:0, - 3, - 7, - 22; reme el 3:2,2,0,2.
Observe que la primera entrada en la fila 2 es cero ahora. Pues usted verá como usted sigue este algoritmo, ésta era la meta de las primeras operaciones en esta matriz.

Intercambio de filas

Cualquier dos filas en la matriz pueden ser intercambiadas sin el cambio del sistema linear representado por la matriz. Mientras que el intercambio de la fila no es necesario para solucionar este sistema de la muestra, es demostrado aquí por las filas de intercambio 2 y 3.

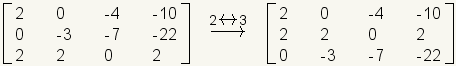1:2,0 de la fila de la matriz, - 4, - 10; reme el 2:-2, - 3, - 3, - 12; reme el 3:2,2,0,2; la flecha que indica la fila 1 más 2 entra la fila 2; 1:2,0 de la fila de la matriz, - 4, - 10; reme el 2:0, - 3, - 7, - 22; reme el 3:2,2,0,2.
La fila que intercambia para solucionar el sistema linear se utiliza generalmente para trasladarse una fila con ceros principales a un punto más conveniente en la matriz.

Combinar operaciones

Las operaciones unas de los se pueden combinar en una sola transformación de la matriz. Tenga cuidado sin embargo, las combinaciones más complicadas de transformaciones puede llevar a los errores. Cualquier error dará resultados falsos. En el ejemplo siguiente, la fila 1 es multiplicada por la negativa 1 y agregada para remar 2.

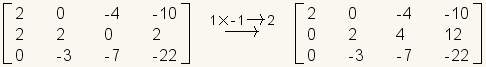1:2,0 de la fila de la matriz, - 4, - 10; reme el 2:0, - 3, - 7, - 22; la flecha del 3:2,2,0,2 de la fila que indica la fila 1 por -1 se agrega para remar 2, que entra la fila 2; 1:2,0 de la fila de la matriz, - 4, - 10; reme el 2:0, - 3, - 7, - 22; reme el 3:2,2,0,2.

El algoritmo

Cada uno de los pasos en este algoritmo se termina usando las operaciones de la fila de la multiplicación escalar de filas, suma de filas, y de intercambiar filas.

El primer paso en solucionar una ecuación linear usando una matriz es conseguir todos los ceros debajo de la diagonal. La orden en la cual éstos se hacen convencionalmente se ilustra aquí:

Fila 1 de la matriz: a_11, a_12, a_13, a_14; fila 2: (1), a_22, a_23, a_24; fila 3: (2), (3), a_33, a_34.

El segundo paso es transformar la matriz de modo que los coeficientes en la diagonal sean todos los. Esto es ilustrada por la matriz siguiente.

1:1 de la fila de la matriz, a_12, a_13, a_14; 2:0,1 de la fila, a_23, a_24; 3:0,0,1 de la fila, a_34.
Esto se llama forma de la fila-eschelon. Una matriz que representa un sistema linear que esté en forma de la fila-eschelon se puede solucionar el resto de la manera usando detrás la substitución.

El tercer paso es transformar la matriz así que las entradas sobre la diagonal son todos los ceros. La matriz siguiente ilustra este paso.

1:1,0,0 de la fila de la matriz, a_14; 2:0,1,0 de la fila, a_24; 3:0,0,1 de la fila, a_34.
Una vez que la matriz está en esta forma, llamada forma reducida del fila-grado, la solución se puede leer de la matriz:
1:1,0,0 de la fila de la matriz, a_14; 2:0,1,0 de la fila, a_24; el 3:0,0,1 de la fila, a_34 implica x=a14;y=a24;z=a34.

Ejemplo (continuo)

Divida la fila 1 y la fila 2 por 2. Esto las hace más fáciles trabajar con.

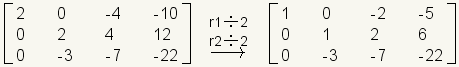1:2,0 de la fila de la matriz, - 4, - 10; 2:0,2,4,12 de la fila; reme el 3:0, - 3, - 7, - la divisoria transformada 22 por 2, fila 2 de la fila 1 dividida por 2 da 1:1,0 de la fila de la matriz, - 2, - 5; reme el 2:0,1,2,6; reme el 3:0, - 3, - 7, - 22.

Multiplique la fila 2 por 3 y agregúela para remar 3.

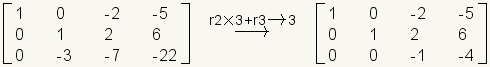1:1,0 de la fila de la matriz, - 2, - 5; 2:0,1,2,6 de la fila; reme el 3:0, - 3, - 7, - la fila transformada 22 2 la fila más 3 del tiempo 3 en la fila 3 da 1:1,0 de la fila de la matriz, - 2, - 5; reme el 2:0,1,2,6; reme el 3:0,0, - 1, - 4.

Multiplique la fila 3 por -1.

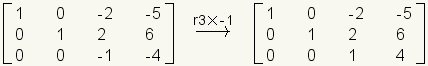1:1,0 de la fila de la matriz, - 2, - 5; 2:0,1,2,6 de la fila; reme el 3:0,0, - 1, - la fila transformada 4 3 por -1 da 1:1,0 de la fila de la matriz, - 2, - 5; reme el 2:0,1,2,6; reme el 3:0,0,1,4.

Multiplique la fila 3 por -2 y agregúela para remar 2 con el resultado en la fila 2.

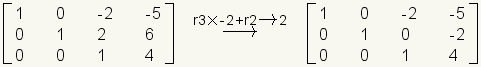1:1,0 de la fila de la matriz, - 2, - 5; 2:0,1,2,6 de la fila; la fila transformada 3:0,0,1,4 3 de la fila por -1 da 1:1,0 de la fila de la matriz, - 2, - 5; 2:0,1,0 de la fila, - 2; 3:0,0,1,4 de la fila.

Multiplique la fila 3 por 2 y agregúela para remar 1 con el resultado en la fila 1.

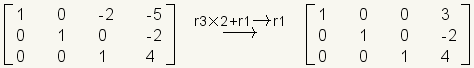1:1,0 de la fila de la matriz, - 2, - 5; 2:0,1,0 de la fila, - 2; la fila transformada 3:0,0,1,4 3 de la fila por -1 da 1:1,0,0,3 de la fila de la matriz; 2:0,1,0 de la fila, - 2; 3:0,0,1,4 de la fila.

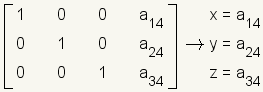
Lea la solución de la matriz.

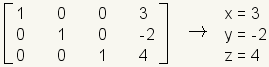1:1,0,0,3 de la fila de la matriz; 2:0,1,0 de la fila, - 2; el 3:0,0,1,4 de la fila da x=3, y=-2, z=4.

Clases de soluciones

Exactamente una solución: Un sistema linear con exactamente una solución tendrá una diagonal de unas, y los ceros del resto a excepción de la columna de derecha:

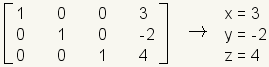1:1,0,0,3 de la fila de la matriz; 2:0,1,0 de la fila, - 2; el 3:0,0,1,4 de la fila da x=3, y=-2, z=4.

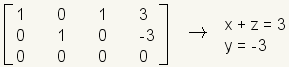
Soluciones infinitas: Un sistema linear con las soluciones infinitas tendrá una fila de todos los ceros, y no se puede reducir a la forma reducida del eschelon:

1:1,0,1,3 de la fila de la matriz; 2:0,1,0 de la fila, - 3; el 3:0,0,0,0 de la fila da x+z=3, y=-3.

Ninguna solución: Un sistema linear sin la solución tendrá una fila con todos los ceros a excepción de la entrada pasada. Ésta es la declaración matemática 0=7, que es imposible. Tan no hay solución.

1:1,0,1,3 de la fila de la matriz; 2:0,1,0 de la fila, - 3; 3:0,0,0,7 de la fila ninguna solución.

Citar este artículo como:
Usando las matrices para solucionar sistemas lineares. 2009-04-03. Enciclopedia de Todas las Palabras de la Matemáticas. Life is a Story Problem.org. http://www.allmathwords.org/es/m/matrixlinearsystem.html.

Traducciones

créditos de imagen

  • Todas las imágenes y manipulatives están por David McAdams a menos que estén indicadas de otra manera. Todas las imágenes de David McAdams son & de los derechos reservados; © Life is a Story Problem.org y se puede reproducir para el uso educativo no comercial solamente.

La historia de revisión


2009-04-03: Traducido automáticamente por BabelFish. (babelfish.yahoo.com.)
2008-12-23: Deletreo corregido (McAdams, David.)
2008-12-16: Versión inicial (McAdams, David.)

Enciclopedia de Todas las Palabras de la Matemáticas es un servicio de Life is a Story Problem.org.
Los derechos reservados ©2005-2009 de Life is a Story Problem.org. Todos los derechos reservados.
Creative Commons License Este trabajo se autoriza debajo de una Creative Commons Attribution-Noncommercial-Share Alike 3.0 License