Ecuación cuadrático
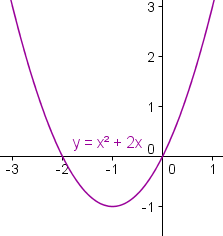 | | Cuadro 1: Gráfico de la ecuación cuadrático f(x) = x2 + 2x. |
|
| | El manipulante 1: Ecuación cuadrático. Creado con GeoGebra. |
Una ecuación cuadrático es una
ecuación
de un
polinomio
del
grado
dos. Cuando está representada gráficamente, una ecuación cuadrático hace una
parábola
con una directriz horizontal. El cuadro 1 demuestra un gráfico de la
ecuación cuadrático f(x) = x2 + 2x.
La forma estándar de una ecuación cuadrático es
f(x) = ax2 + bx + c donde a, b y c
están coeficientes constantes y a ≠ 0. La ecuación en el cuadro 1
puesto en forma estándar es f(x) = x2 + 2x + 0. El
manipulante 1 demuestra el gráfico de una ecuación cuadrático usando el
estándar de. Chasque encendido los puntos rojos en los resbaladores en el
manipulante 1 para cambiar la figura. Chasque encendido el botón
 de reajuste para cambiar la figura de nuevo a su configuración original.
de reajuste para cambiar la figura de nuevo a su configuración original.
Descubrimiento
- Mueva el resbalador para hasta a=0. ¿Cuál es el resultado?
¿Por qué la condición a≠0 se pone en la ecuación cuadrático?
- ¿Qué cambia en el gráfico cuando se cambia a?
- ¿Qué cambia en el gráfico cuando se cambia b?
- ¿Qué cambia en el gráfico cuando se cambia c?
Ejemplos de ecuaciones cuadráticos |
| Ecuaciones cuadráticos | Razón |
|---|
| y = 3x2 - 2x - 4 | La función es un polinomio del grado 2. |
| y = -x2 - 3 | La función es un polinomio del grado 2. |
| g = b2 | La función es un polinomio del grado 2. |
| y = sin(π/2)x2 + 4 | La función es un polinomio del grado 2. Puesto que la discusión de la función del seno es un constante, la función sí mismo es un constante y se puede tratar como cualquier otro coeficiente. |
| r = (t-1)(t+3) | El derecho de la ecuación se puede ampliar usando la propiedad distributiva de la multiplicación sobre la suma y la resta para rendir r = t2 + 2t - 3, que es un polinomio del grado 2. |
Ejemplos de las ecuaciones que no son cuadráticos |
| ecuaciones No-cuadráticos | Razón |
|---|
| y = 3x3 + 2x2 - x + 3 | La función es un polinomio del grado 3, así que no es cuadrático. |
| y = x2 - sin(x) + 3 | Desde pecado (x) está en la ecuación, él no es un polinomio. |
| w = 3m - 4 | La función es un polinomio del grado 1, así que no es cuadrático. |
| y = log(2x2 - x + 3) | Puesto que la ecuación contiene un logaritmo con una discusión variable, no es un polinomio. |
| y = x(x-2)(x+1) | El derecho de la ecuación se puede ampliar a y = x3 - x2 - 2x, que es un polinomio del grado 3. |
| Cuadro 1 |
|
Discriminante de una ecuación cuadrático
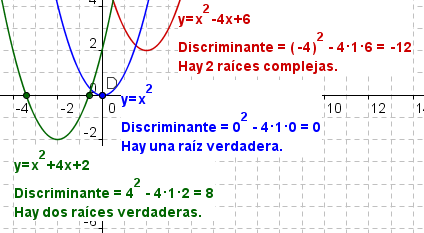
| | Cuadro 2: Discriminants de ecuaciones cuadráticos. |
|
El discriminante de una ecuación cuadrático se utiliza para determinar si una ecuación cuadrático tiene raíces verdaderas o complejas. La expresión para el discriminante es
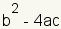 . |
Para una ecuación cuadrático en la forma
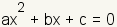
, la solución se puede encontrar usando la
fórmula cuadrático 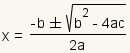
.
Una ecuación cuadrático puede tener 2 raíces real, 1 raíz real, o 2 raíces complejas (véase
discriminante).
Ejemplo 1: Dos raíces verdaderas.
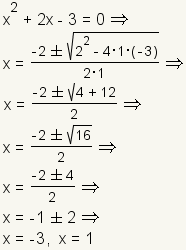
| 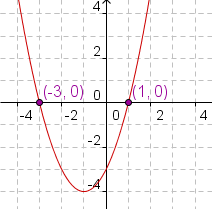 | | Cuadro 3: Gráfico de x2+2x-3. |
|
Ejemplo 2: Una raíz verdadera.
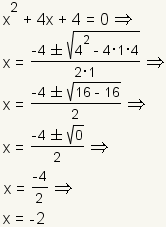
| 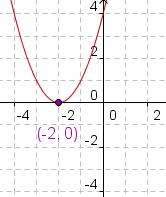 | | Cuadro 4: Gráfico de x2+4x+4. |
|
Ejemplo 3: Dos raíces complejas.
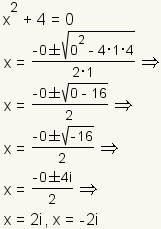
| 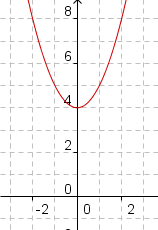 | | Cuadro 5: Gráfico de x2+4=0. |
|
Formas de ecuaciones cuadráticos
|
| | El manipulante 2: Función parabólica - forma normal. Manipulante creado con GeoGebra. |
|
La forma estándar una ecuación parabólica es
y = ax2 + bx + c. En el manipulante 2, chasque encendido los
puntos en los resbaladores rojos y arrástrelos para cambiar la figura.
Descubrimiento
- Chasque encendido el punto para el resbalador etiquetado “a�? y arrástrelo. ¿Qué cambia si “a�? es negativa, cero o positivo?
- Chasque encendido el punto para el resbalador etiquetado “b�? y arrástrelo. ¿Qué cambia como cambios de “b�??
- Chasque encendido el punto para el resbalador etiquetado “c�? y arrástrelo. ¿Qué cambia como cambios de “c�??
|
|
| | El manipulante 3: Función parabólica - x-intercepte la forma. Manipulante creado con GeoGebra. |
|
x-intercepte
la forma de una ecuación parabólica es y = a(x-x0)(x-x1)
donde está x0 uno intercepta de la ecuación cuadrático,
x1 es el otro x-intercepta, y a indica cómo es
escarpado son los lados de la ecuación cuadrático. Si
x0 = x1, la ecuación cuadrático intercepta
el abscisa solamente una vez. No todas las ecuaciones cuadráticos se pueden
describir usando x-interceptan la forma.
El manipulante 3 demuenstra una ecuación cuadrático con los elementos
del x-interceptan la forma. Chasque encendido x-intercepta xi0
y xi1 etiquetados y los arrastra para cambiar la figura.
Chasque encendido el punto etiquetado a en el resbalador y arrástrelo
para cambiar la figura.
Descubrimiento
- Chasque encendido los puntos azules etiquetados xi0 y xi1 y arrástrelos. ¿Cómo cambian la figura?
- Chasque encendido el punto rojo en el resbalador etiquetado a y arrástrelo. ¿Cómo cambia la figura?
- ¿Puede usted utilizar el manipulante 3 para demostrar una ecuación cuadrático que no intercepte el abscisa? ¿Por qué o por qué no?
|
|
| | 4 manipulantes: Función parabólica en forma de la vértice. Manipulante creado con GeoGebra. |
|
La forma de la vértice de una ecuación parabólica es
y-y0 = a (x-x0)2. La
vértice de la ecuación cuadrático está en el punto
(x0, y0). demostraciones cómo es escarpado
son los lados de la ecuación cuadrático. Chasque encendido los puntos en los
resbaladores en 4 manipulantes y arrástrelos para cambiar la figura.
Descubrimiento
- Chasque encendido los resbaladores para x0 y el y0 y arrástrelos. ¿Qué cambia sobre la ecuación cuadrático?
- Chasque encendido el resbalador para a y arrástrelo. ¿Qué cambia sobre la ecuación cuadrático?
- ¿Si y-y0 = a (x-x0)2 es la
ecuación de la ecuación cuadrático, cuál es la ecuación de la recta de simetría?
|
|
| | El manipulante 5: Función parabólica en forma cónica. Manipulante creado con GeoGebra. |
La forma de la sección cónica de una ecuación
parabólica esta Ax2 + Bxy + Cy2 + Dx + Ey + F = 0
donde B2 = 4AC y el A ≠ 0 o el C ≠ 0.
Esta forma permite que una dibuje ecuaciones cuadráticos donde no está paralela
la directriz al abscica o al ordenata. Los resbaladores en el manipulante 5
permiten que usted cambie la figura. Observe que para algunos valores de
A a F, la ecuación cuadrático estará fuera de la zona
de visualización del gráfico.
Descubrimiento
- Los criterios para la sección cónica forman de un parabólico son el A ≠ 0 o el C ≠ 0. ¿Qué sucede si A y C son 0?
- ¿Qué dirección la parábola abre si C = 0? Cerciórese de cambiar A a positivo y a la negativa para conseguir el cuadro completo.
- ¿Qué dirección la parábola abre si A = 0? Cerciórese de cambiar C a positivo y a la negativa para conseguir el cuadro completo.
|
Representación gráfica de una ecuación gráficamente cuadrático
El gráfico de una ecuación cuadrático se puede
dibujar usando la definición de una parábola: Todos los puntos en un plano
equidistante
de una recta, llamada la directriz, y un punto,
llamado el foco, que no está en la recta. Cada
ecuación cuadrático también tiene una
vértice
y una
recta de simetría.
Descubrimiento
En el manipulante 6, chasque encendido el foco y el punto rojo en la directriz
y arrástrelos cambio la figura.
- ¿Cómo es la ecuación cuadrático diferente si el foco y la directriz son cercanos juntos en comparación con lejos aparte?
- ¿Cómo la ecuación cuadrático cambia si el foco se mueve a la izquierda o a la derecha?
- Chasque encendido el foco (punto púrpura) y arrástrelo hasta que el foco esté en la directriz. ¿Qué sucede a la ecuación cuadrático? Cuando sucede esto, los matemáticos dicen que la recta es una ecuación cuadrático degenerada.
Partes de una parábola
|
| | El manipulante 6: Partes de una parábola creado con GeoGebra. |
La vértice de una ecuación cuadrático está en el punto de la inflexión de
la ecuación cuadrático. El punto de la inflexión es el punto donde la curva
parabólica cambia la dirección. En el manipulante 6, la vértice es azul. La
vértice no se puede arrastrar en este manipulante, porque la vértice es
dependiente sobre el foco y la directriz. Chasque encendido las cajas de cheque
en manipulante 6 para ver las partes de una ecuación cuadrático.
La distancia del foco a cualquier punto en la ecuación cuadrático es igual
que la distancia de ese punto a la directriz. Chasque encendido el punto azul
en la ecuación cuadrático y arrástrelo para demostrar esta propiedad.
|
Más información
- McAdams, David. Parábola. allmathwords.org. Life is a Story Problem.org. 2009-04-17. http://www.allmathwords.org/article.aspx?lang=es&id=Parabola.
- cuadrado. buscon.rae.es. Real Academia Española. 2009-04-17. http://buscon.rae.es/draeI/SrvltConsulta?TIPO_BUS=3&LEMA=cuadrado.
Citar este artículo como:
Ecuación cuadrático. 2009-04-03. Enciclopedia de Todas las Palabras de la Matemáticas. Life is a Story Problem.org. http://www.allmathwords.org/es/q/quadraticequation.html.
Traducciones
créditos de imagen
- Todas las imágenes y manipulatives están por David McAdams a menos que estén indicadas de otra manera. Todas las imágenes de David McAdams son & de los derechos reservados; © Life is a Story Problem.org y se puede reproducir para el uso educativo no comercial solamente.
La historia de revisión
2009-04-03: Traducido automáticamente por
BabelFish. (
babelfish.yahoo.com.)
2009-01-22: Figura agregada a la sección en discriminants (
McAdams, David.)
2008-12-10: Sección agregada en discriminante, soluciones a una ecuación cuadrático (
McAdams, David.)
2008-10-19: Versión inicial (
McAdams, David.)
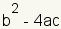 .
.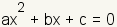 , la solución se puede encontrar usando la fórmula cuadrático
, la solución se puede encontrar usando la fórmula cuadrático 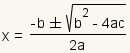 .
.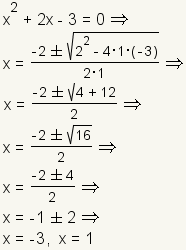
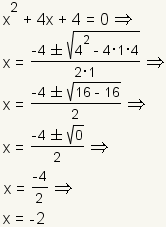
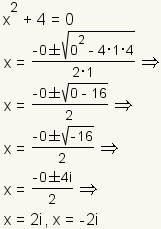
 Este trabajo
se autoriza debajo de una
Creative Commons Attribution-Noncommercial-Share Alike 3.0 License
Este trabajo
se autoriza debajo de una
Creative Commons Attribution-Noncommercial-Share Alike 3.0 License

 de reajuste para cambiar la figura de nuevo a su configuración original.
de reajuste para cambiar la figura de nuevo a su configuración original.



