Sistema de ecuaciones

y = x2 - 3
y = 2x + 1
Cuadro 1: Un sistema de ecuaciones

Un sistema de ecuaciones es un conjunto de las ecuaciones que se toman para ser simultáneamente verdades. Si un sistema de ecuaciones contiene solamente ecuaciones lineares es un sistema linear.

Un sistema de ecuaciones no puede tener ninguna solución. Esto significa que no hay valores para los cuales todas las ecuaciones son verdades inmediatamente. Un sistema de ecuaciones puede tener una o más soluciones. Las soluciones del sistema de ecuaciones son cualquier valor para las cuales todas las ecuaciones sean simultáneamente verdades.

Visualización de un sistema de ecuaciones

Lo sentimos, pero la GeoGebra Applet no se pudo iniciar. Por favor, asegúrese de que Java 1.4.2 (o posterior) está instalado y activo en su navegador ( Haga clic aquí para instalar Java ahora )
El manipulante 1: Sistema de ecuaciones. Creado con GeoGebra.

Un sistema de ecuaciones puede ser visualizado representando las ecuaciones gráficamente. Las soluciones del sistema son los puntos de las intersecciones de las curvas. Si los gráficos de las ecuaciones no se intersecan, el sistema no tiene ninguna solución.

La figura en 1 manipulante demuestra dos ecuaciones simultáneas. La parábola es verde y la recta es azul. Los puntos rojos son los puntos de la intersección. Los valores de los puntos rojos son las soluciones al sistema. Chasque encendido la recta y la parábola y arrástrelas para cambiar la figura.

Descubrimiento

Chasque encendido la parábola en el manipulante 1 y arrástrela de modo que haya solamente una solución. Chasque encendido la parábola y arrástrela de modo que no haya soluciones. Para reajustar la figura a su configuración inicial, chasque encendido el botón de reajuste (Botón de reajuste de GGB).

¿Cuál es el número más grande de soluciones que se puedan encontrar para un sistema que consiste en una recta y una parábola?

El solucionar de Substitution

Un sistema de ecuaciones se puede solucionar a menudo por la substitución. Una variable es substituida por una expresión igual a esa variable. Tome el sistema de ecuaciones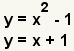
y=x^2-1, y=x+1

PasoEcuacionesDescripción
1y=x^2-1, y=x+1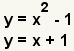Éstas son las ecuaciones simultáneas a solucionar.
2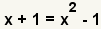x+1=x^2-1Utilice la propiedad de la substitución de la igualdad para substituir x+1 adentro para el y.
3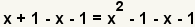x+1-x-1=x^2-1-x-1Puesto que la ecuación resultante en el paso 2 es una ecuación cuadrática, utilizaremos la fórmula cuadrático para solucionarla. La fórmula cuadrático requiere un cero esté en un lado de la ecuación. Utilice la propiedad aditiva de la igualdad para agregar -x-1 a ambos lados.
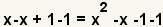x-x+1-1=x^2-x-1-1Utilice la propiedad asociativa de la suma para conseguir términos semejantes al lado de uno a.
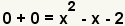0+0=x^2-x-2Combine términos semejantes.
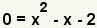0=x^2-x-2Utilice la propiedad aditiva de cero para simplificar el lado izquierdo de la ecuación.
4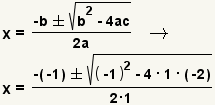x= ((- b+-square raíz (b^2-4*a*c))/(2*a) implica el x= ((- (- 1) raíz de +-square ((- 1) ^2-4*1* (- 2)))/(2*1)Aplique la fórmula cuadrático con a=1, b=-1 y c=-2.
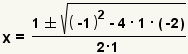x= ((raíz 1+-square ((- 1) ^2-4*1* (- 2)))/(2*1)Utilice la definición de la negada para simplificar la negativa doble.
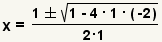x= ((raíz 1+-square (1-4*1* (- 2)))/(2*1)Simplifique el exponente.
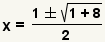x= ((raíz 1+-square (1+8)) /2Simplifique la multiplicación y la división.
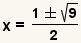x= ((raíz 1+-square (9)) /2Simplifique la suma y la resta.
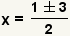x= (1+-3) /2Simplifique la raíz cuadrada.
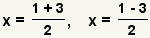x= (1+3)/2, x= (1-3) /2Parta el más o el menos en dos ecuaciones.
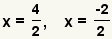x=4/2, x= (- 2) /2Adición y resta partidas.
x=2, x=-1Simplifique las fracciones. Éstos son los valores posibles del x.
5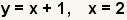y=x+1, x=2Utilice la propiedad de la substitución de la igualdad para substituir 2 adentro para el x.
y=2+1Realice la substitución.
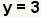y=3Simplifique la suma.
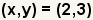(x, y)= (2.3)Una solución del sistema es el par ordenado (2. 3).
6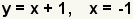y=x+1, x=-1Utilice la propiedad de la substitución de la igualdad para substituir -1 adentro para el x.
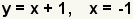y=-1+1Realice la substitución.
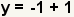y=0Simplifique la suma.
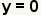(x, y)= (- 1.0)Una solución del sistema es el par ordenado (-1. 0).
Cuadro 1: Solucionar ecuaciones simultáneas

Más información

  • McAdams, David. Sistema linear. AllMathWords.org. Life is a Story Problem.org. 2009-04-03. http://www.allmathwords.org/article.aspx?lang=es&id=Linear%20System.

Citar este artículo como:
Sistema de ecuaciones. 2009-04-03. Enciclopedia de Todas las Palabras de la Matemáticas. Life is a Story Problem.org. http://www.allmathwords.org/es/s/systemofequations.html.

Traducciones

créditos de imagen

  • Todas las imágenes y manipulatives están por David McAdams a menos que estén indicadas de otra manera. Todas las imágenes de David McAdams son & de los derechos reservados; © Life is a Story Problem.org y se puede reproducir para el uso educativo no comercial solamente.

La historia de revisión


2009-04-03: Traducido automáticamente por BabelFish. (babelfish.yahoo.com.)
2009-02-10: Versión inicial (McAdams, David.)

Enciclopedia de Todas las Palabras de la Matemáticas es un servicio de Life is a Story Problem.org.
Los derechos reservados ©2005-2009 de Life is a Story Problem.org. Todos los derechos reservados.
Creative Commons License Este trabajo se autoriza debajo de una Creative Commons Attribution-Noncommercial-Share Alike 3.0 License