Suma: Para ensamblar dos o más cantidades juntas en una suma.

Suma

La suma está ensamblando dos o más cantidades juntas para hacer una suma. El cuadro 1 da un ejemplo de la suma del número entero. En la declaración 4 + 3 = 7 de la suma, 4 y 3 son sumandos y 7 es la suma. Los sumandos son qué se está agregando junto, y la suma es el resultado de la suma.
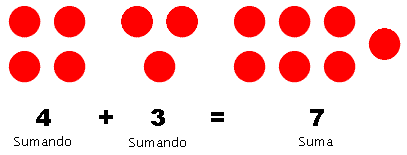4 puntos y 3 puntos y 7 puntos que representan 4 + 3 = 7
Cuadro 1: Representación de 4 + 3 = 7

Los números reales pueden también ser añadiros. El cuadro 2 da una representación de 2 + 1 = 3.
Recta numérica que demuestra 2 + 1 = 3
Cuadro 2: Representación de 2 + 1 = 3

El manipulante 3 representando la suma de números reales. Chasque encendido los puntos amarillos y arrástrelos para cambiar la figura.
Lo sentimos, pero la GeoGebra Applet no se pudo iniciar. Por favor, asegúrese de que Java 1.4.2 (o posterior) está instalado y activo en su navegador ( Haga clic aquí para instalar Java ahora )
El manipulante 3: Adición de números reales creados con GeoGebra.

La suma también se define para muchos tipos de entidades de la matemáticas tales como vectores y matrices.

Resta

Los matemáticos definen generalmente la resta como suma de lo contrario del añadido de un valor. La resta se define esta manera de modo que la resta de vectores y las matrices y otras entidades de la matemáticas tenga más sentido. Indicado matemáticamente, a - b = a + -b. Una diferencia es el resultado de restar un número de otro. Por ejemplo, en la ecuación 7 - 4 = 3, 3 es la diferencia.

Un ejemplo de esto es 5 - 4 = 5 + -4 = 1

Características de la suma de números reales

Nombre de propiedadEjemploDescripción
Característica de la suma por 0a + 0 = aCualquier número real más cero iguala el número original. 0 es la identidad aditiva para los números reales.
Característica asociativa de la sumaa + (b + c) = (a + b) + cLa orden de en qué adiciones múltiples de números reales se realizan no cambia el resultado.
Característica comutativa de la sumaa + b = b + aNo importa que de dos números vienen primero además de números reales.
Característica distributiva de la multiplicación sobre la suma y la restaa(b + c) = ab + acLa multiplicación es distributiva sobre la suma y la resta.
Cuadro 1: Características de la suma

Más información

  • suma. buscon.rae.es. Real Academia Española. 2009-04-03. http://buscon.rae.es/draeI/SrvltConsulta?TIPO_BUS=3&LEMA=adición.
  • sustracción. buscon.rae.es. Real Academia Española. 2009-04-03. http://buscon.rae.es/draeI/SrvltConsulta?TIPO_BUS=3&LEMA=sustracción.

Citar este artículo como:
Suma. 2009-04-03. Enciclopedia de Todas las Palabras de la Matemáticas. Life is a Story Problem LLC. http://www.allmathwords.org/es/a/addition.html.

Traducciones

créditos de imagen

  • Todas las imágenes y manipulatives están por David McAdams a menos que estén indicadas de otra manera. Todas las imágenes de David McAdams son & de los derechos reservados; © Life is a Story Problem LLC y se puede reproducir para el uso educativo no comercial solamente.

La historia de revisión


2009-04-03: Traducido automáticamente por BabelFish. (babelfish.yahoo.com.)
2009-03-03: Discusión agregada de la diferencia a la sección en la substracción (McAdams, David.)
2008-09-16: Cuadro cambiado 3 a un manipulante (McAdams, David.)
2008-06-07: Faltas de mecanografíia corregidas (McAdams, David.)
2008-05-14: Versión inicial (McAdams, David.)

Enciclopedia de Todas las Palabras de la Matemáticas es un servicio de Life is a Story Problem LLC.
Los derechos reservados ©2005-2009 de Life is a Story Problem LLC. Todos los derechos reservados.
Creative Commons License Este trabajo se autoriza debajo de una Creative Commons Attribution-Noncommercial-Share Alike 3.0 License