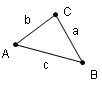
Triángulo
Un triángulo es un polÃgono trilátero. Todos los triángulos tienen tres lados no-colineales compuestos de la recta segmentos recta. Todos los triángulos tienen tres ángulos.
|
|
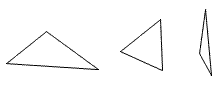
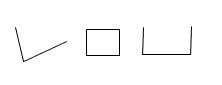
| Cuadro 1: Ejemplos de triángulos | Cuadro 2: Ejemplos de las formas que no son triángulos. |
Ã?ndice del artÃculo
Tipos de triángulos
Triángulo rectángulo
Triángulo acutángulo
triángulo obtusángulo
Triángulo escaleno
Triángulo equilátero
Triángulo isósceles
Triángulos de etiquetado
Propriedades de triángulos
PerÃmetro de un triángulo
Suma de ángulos de un triángulo
�rea de un triángulo
Fórmula de Herón para el área de un triángulo
Circunferencia inscrita e Incentro de un triángulo
Circunferencia circunscrita y circuncentro de un riángulo
Punto medio de un triángulo
Centro de figura de un triángulo
Altitud de un triángulo
Orthocenter de un triángulo
Congruencia del LAL
Euclid. Los elementos, reservan 1 asunto 6: Si dos lados de un triángulo son iguales, los ángulos enfrente de los lados iguales son iguales.
Centros de un triángulo
Tipos de triángulos
| Ejemplo | Tecleo conocido para más información. | Descripción |
 | Triángulo rectángulo | Un triángulo con uno de ángulo recto. |
 | Triángulo agudo | Un triángulo con tres ángulos agudos. |
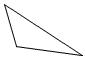 | Triángulo obtuso | Un triángulo con un ángulo obtuso. |
 | Triángulo escaleno | Un triángulo cuyos lados son todos diversas longitudes. |
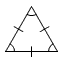 | Triángulo equilátero | Un triángulo con tres lados iguales. |
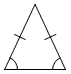 | Triángulo isósceles | Un triángulo con dos lados iguales. |
| Cuadro 3: Tipos de triángulos | ||
Triángulos de etiquetado
| De la convención, los triángulos se etiquetan generalmente en una dirección a la izquierda, a menudo usando las letras A, B, y C. Los lados se etiquetan a menudo con una letra minúscula que corresponde a la vértice enfrente del lado. |
Propriedades de triángulos
| PerÃmetro |
| El perÃmetro de un triángulo es los lados del triángulo o de la suma de las longitudes de los lados. Por ejemplo, si las longitudes de los lados son 3, 4, y 5, el perÃmetro es 3 + 4 + 5 = 12. Chasque encendido los puntos azules en el manipulante 1 y arrástrelos para cambiar la figura. | ||
| Suma de ángulos |
| En geometrÃa euclidiana, la suma de los ángulos de un triángulo es 180° = 2π. En otras geometrÃas, esto no pudo ser verdad. Chasque encendido los puntos azules en el manipulante 2 y arrástrelos para cambiar la figura. | ||
| Ã?rea |
| El área de un triángulo es a = 1/2 b·h donde está cualquier lado b (base) del triángulo, y h (altura) es la distancia de la vértice enfrente de la base (en este caso B) a la base extendida (en este caso la recta AC). Chasque encendido los puntos azules en el manipulante 3 y arrástrelos para cambiar la figura. | ||
|
El área de un triángulo se puede también calcular de la longitud de los tres lados usando la fórmula de la garza. Primero, uno debe calcular el semiperimeter. Este 1/2 del perÃmetro. Puesto que es el perÃmetro a + b + c donde están la longitud a, b y c de los lados del triángulo, el semiperimeter es s = (1/2)(a+b+c). La fórmula de Héron para el área de un triángulo es área = √(s(s - a)(s - b)(s - c)). | |||
|
Circunferencia inscrita Incentro |
| El circunferencia inscrita de un triángulo es el circunferencia que es tangente a cada uno de los lados de un triángulo. El incentro es el centro del circunferencia inscrita. Para más información sobre el incentro de un triángulo, vea incentro de toda la enciclopedia de las palabras de la matemáticas. Chasque encendido los puntos azules en el manipulante y arrástrelo para cambiar la figura. | ||
| Circunferencia Circunscrita
Circuncentro |
|
El circunferencia circunscrita de un triángulo es el circunferencia que pasa con todas las vértices de un triángulo. El circuncentro es el centro del circunferencia circunscrita. Para más información sobre el circuncentro o el circunferencia circunscrita de un triángulo, vea Circumcenter de Enciclopedia de Todas las Palabras de la Matemáticas. | ||
| Punto medio del triángulo Centro de figura del triángulo |
|
Un punto medio de un triángulo es una recta dibujada con una vértice del triángulo y el punto medio del lado opuesto. Esto significa que cada triángulo tiene tres puntos medios. Los puntos medios de una reunión del triángulo en un punto llamaron el centro de figura del triángulo. El centro de figura de un triángulo es el centro de gravedad del triángulo. Esto significa que si un triángulo es equilibrado en un perno en el centro de figura, serÃa perfectamente equilibrado. El centro de figura de un triángulo es encontrado dibujando dos puntos medios del triángulo. El centro de figura es en el punto donde los puntos medios se intersecan. | ||
| Altitud del triángulo |
| Una altitud de un triángulo es una recta segmento de una vértice del triángulo al extendido enfrente de lado, perpendicular al lado opuesto. | ||
| Triángulo Orthocenter |
| El orthocenter de un triángulo está en la intersección de las altitudes de un triángulo. | ||
| Congruencia del SAS |
|
Dos triángulos son congruentes si dos lados adyacentes y el ángulo contenido por los lados son congruentes con los lados y el ángulo correspondientes del otro triángulo. En este caso decimos que los triángulos son SAS congruente. El SAS representa el lado, ángulo, lado. Para más información sobre congruencia del SAS, vea la congruencia del SAS de toda la enciclopedia de las palabras de la matemáticas. | ||
| Proponga 6, elementos de Euclid: Si dos ángulos de un triángulo son iguales, los lados enfrente de los ángulos iguales son también iguales. |
|
En un triángulo, si dos ángulos tienen longitud igual, los lados enfrente de los ángulos iguales son también iguales. En el cuadro 16, el ABC del ángulo es igual al ángulo ACB. El lado AB es también igual a la CA del lado. Para más información sobre esta propiedad de triángulos vea:
|
Centros de un triángulo
| El manipulante 12: Centros de un triángulo. Creado con GeoGebra. |
Cheque de comprensión
Escriba su respuesta en un trozo de papel, después utilice su ratón para chascar encendido “tecleo para el texto de la respuesta� para ver la respuesta correcta. Chasque encendido los puntos amarillos y arrástrelos para cambiar el manipulante
- ¿Para qué tipo de triángulo los cinco centros se demuestran el mismo punto? Tecleo para la respuesta. Triángulo equilátero.
- ¿Qué centros están siempre dentro de un triángulo? Tecleo para la respuesta. Centroide y incentro.
- ¿Dentro qué centros puede estar o fuera de un triángulo? Tecleo para la respuesta. Centro del circunferencia de los nueve puntos, circuncentro, ortocentro
- ¿Qué centro está en la hipotenusa de un triángulo correcto? Tecleo para la respuesta. Circuncentro
- ¿Qué centro está en la cima enfrente de la hipotenusa de un triángulo correcto? Tecleo para la respuesta. Ortocentro
- ¿Qué centros son siempre colineal (en la misma recta)? Tecleo para la respuesta. Centro del circunferencia de los nueve puntos, centroide, circuncentro, y el ortocentro
- ¿Para qué tipo de triángulo es el ortocentro dentro del triángulo? ¿Tecleo para la respuesta. Triángulo agudo. Fuera del triángulo? Tecleo para la respuesta. Triángulo obtuso
Más información
- McAdams, David. Ã?ngulo. AllMathWords.org. Life is a Story Problem.org. 2009-04-03. http://www.allmathwords.org/article.aspx?lang=es&id=Angle.
- triángulo. buscon.rae.es. Real Academia Española. 2009-04-03. http://buscon.rae.es/draeI/SrvltConsulta?TIPO_BUS=3&LEMA=triángulo.
Citar este artÃculo como:
Triángulo. 2009-04-03. Enciclopedia de Todas las Palabras de la Matemáticas. Life is a Story Problem.org. http://www.allmathwords.org/es/t/triangle.html.
Traducciones
créditos de imagen
- Todas las imágenes y manipulatives están por David McAdams a menos que estén indicadas de otra manera. Todas las imágenes de David McAdams son & de los derechos reservados; © Life is a Story Problem.org y se puede reproducir para el uso educativo no comercial solamente.
La historia de revisión
2009-04-03: Traducido automáticamente por BabelFish. (babelfish.yahoo.com.)
2008-10-30: Cambió todos los manipulatives a GeoGebra (McAdams, David.)
2008-09-15: Wikipedia agregado a más información (McAdams, David.)
2008-06-07: Faltas de mecanografÃia corregidas (McAdams, David.)
2008-03-20: Definición aclarada del triángulo escaleno (McAdams, David.)
2007-08-29: “Centros agregados de un triángulo� (McAdams, David.)
2007-08-24: Ampliado (McAdams, David.)
2007-07-12: Versión inicial (McAdams, David.)
- Navegación
- Home
- Contenido
-
# A B C D E F G H I J L M N O P Q R S T U V X Y - Ayudas del profesor
- Demostraciones de la Clase
- Referencia recÃproca
- GeometrÃa de NYSDE
- LIASP
- LIASP Home
- Condiciones del uso
- PolÃtica de aislamiento
- Done a LIASP
- Estructura de la ayuda este sitio
- Sobre LIASP
- LIASP del Contacto
Enciclopedia de Todas las Palabras de la Matemáticas es un servicio de
Life is a Story Problem.org.
Los derechos reservados ©2005-2009 de Life is a Story Problem.org. Todos los derechos reservados.
Este trabajo
se autoriza debajo de una
Creative Commons Attribution-Noncommercial-Share Alike 3.0 License